Содержание
Инженерная графика | Лекции | Аксонометрические проекции
По вопросам репетиторства по инженерной графике (черчению), вы можете связаться любым удобным для вас способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1250 р./ак.ч.
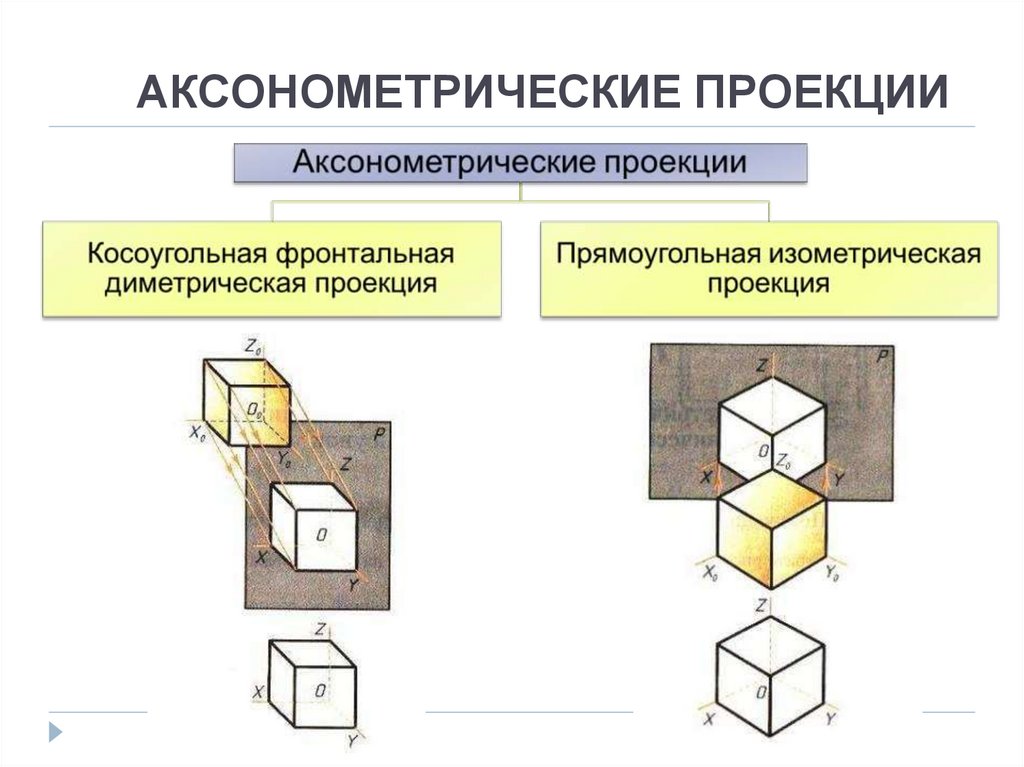
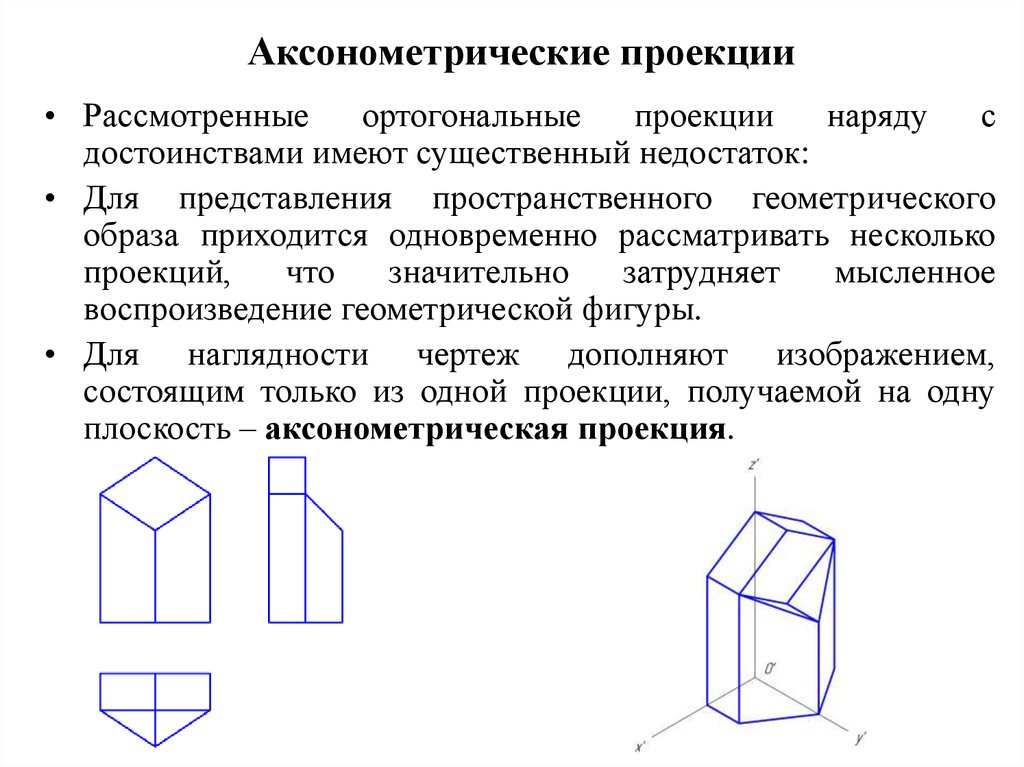
Во многих случаях при выполнении технических чертежей оказывается полезным наряду изображением предметов в системе ортогональных проекций иметь более наглядные изображения. Для построения таких изображений применяются проекции, называемые аксонометрическими.
Способ аксонометрического проецирования состоит в том, что данный предмет вместе с осями прямоугольных координат, к которым эта система относится в пространстве, параллельно проецируется на некоторую плоскость α (Рисунок 4.1).
Рисунок 4.1<>p/
Направление проецирования S определяет положение аксонометрических осей на плоскости проекций α, а также коэффициенты искажения по ним. При этом необходимо обеспечить наглядность изображения и возможность производить определения положений и размеров предмета.
В качестве примера на Рисунке 4.2 показано построение аксонометрической проекции точки А по ее ортогональным проекциям.
Рисунок 4.2
Здесь буквами k, m, n обозначены коэффициенты искажения по осям OX, OY и OZ соответственно. Если все три коэффициента равны между собой, то аксонометрическая проекция называется изометрической, если равны между собой только два коэффициента, то проекция называется диметрической, если же k≠m≠n, то проекция называется триметрической.
Если направление проецирования S перпендикулярно плоскости проекций α, то аксонометрическая проекция носит названия прямоугольной. В противном случае, аксонометрическая проекция называется косоугольной.
ГОСТ 2.317-2011 устанавливает следующие прямоугольные и косоугольные аксонометрические проекции:
- прямоугольные изометрические и диметрические;
- косоугольные фронтально изометрические, горизонтально изометрические и фронтально диметрические;
Ниже приводятся параметры только трех наиболее часто применяемых на практике аксонометрических проекций.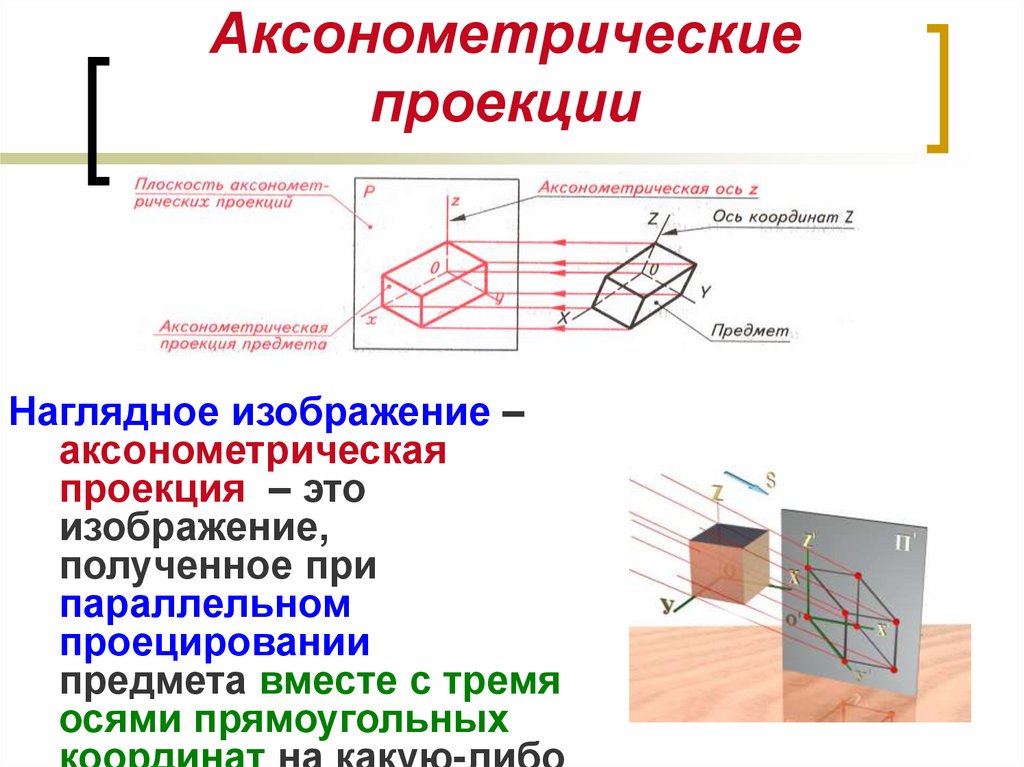
Каждая такая проекция определяется положением осей, коэффициентами искажения по ним, размерами и направлениями осей эллипсов, расположенных в плоскостях, параллельных координатным плоскостям. Для упрощения геометрических построений коэффициенты искажения по осям, как правило, округляются.
4.1. Прямоугольные проекции
4.1.1. Изометрическая проекция
Направление аксонометрических осей приведено на Рисунке 4.3.
Рисунок 4.3 – Аксонометрические оси в прямоугольной изометрической проекции
Действительные коэффициенты искажения по осям OX, OY и OZ равны 0,82. Но с такими значениями коэффициентов искажения работать не удобно, поэтому, на практике, используются приведенные коэффициенты искажений. Эта проекция обычно выполняется без искажения, поэтому, приведенные коэффициенты искажений принимается k = m = n =1. Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются в эллипсы, большая ось которых равна 1,22, а малая – 0,71 диаметра образующей окружности D.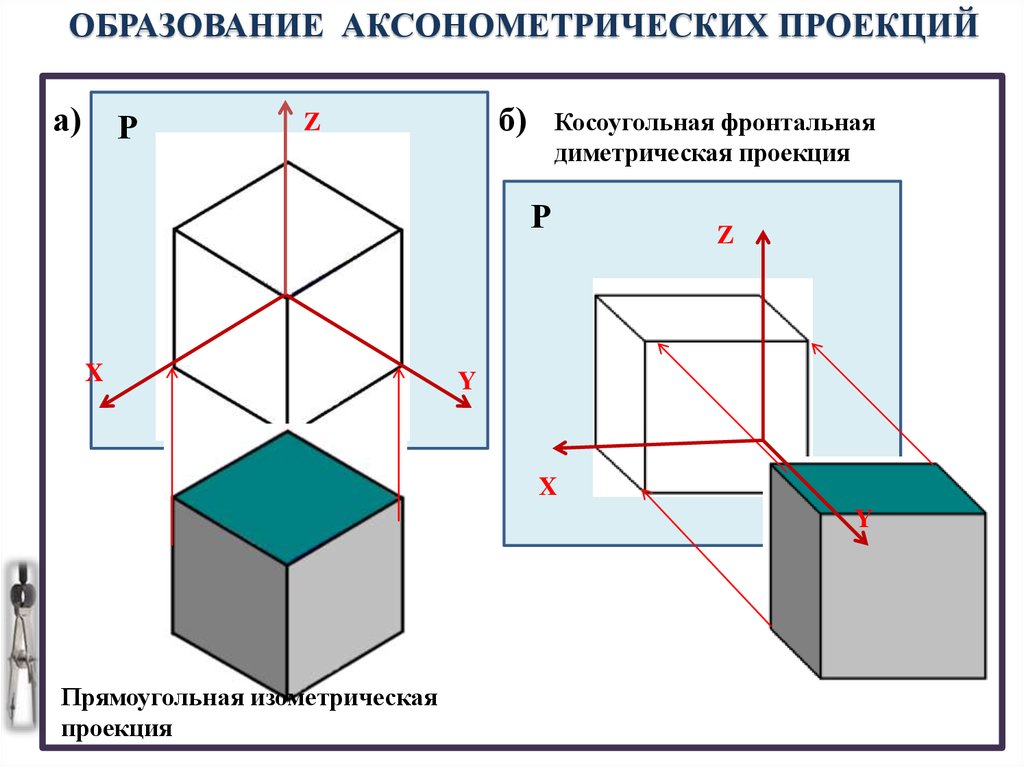
Большие оси эллипсов 1, 2 и 3 расположены под углом 90º к осям OY, OZ и OX, соответственно.
Пример выполнения изометрической проекции условной детали с вырезом приводится на Рисунке 4.4.
Рисунок 4.4 – Изображение детали в прямоугольной изометрической проекции
4.1.2. Диметрическая проекция
Положение аксонометрических осей проводится на Рисунке 4.5.
Для построения угла, приблизительно равного 7º10´, строится прямоугольный треугольник, катеты которого составляют одну и восемь единиц длины; для построения угла, приблизительно равного 41º25´ — катеты треугольника, соответственно, равны семи и восьми единицам длины.
Коэффициенты искажения по осям ОХ и OZ k=n=0,94 а по оси OY – m=0,47. При округлении этих параметров принимается k=n=1 и m=0,5. В этом случае размеры осей эллипсов будут: большая ось эллипса 1 равна 0,95D и эллипсов 2 и 3 – 0,35D (D – диаметр окружности).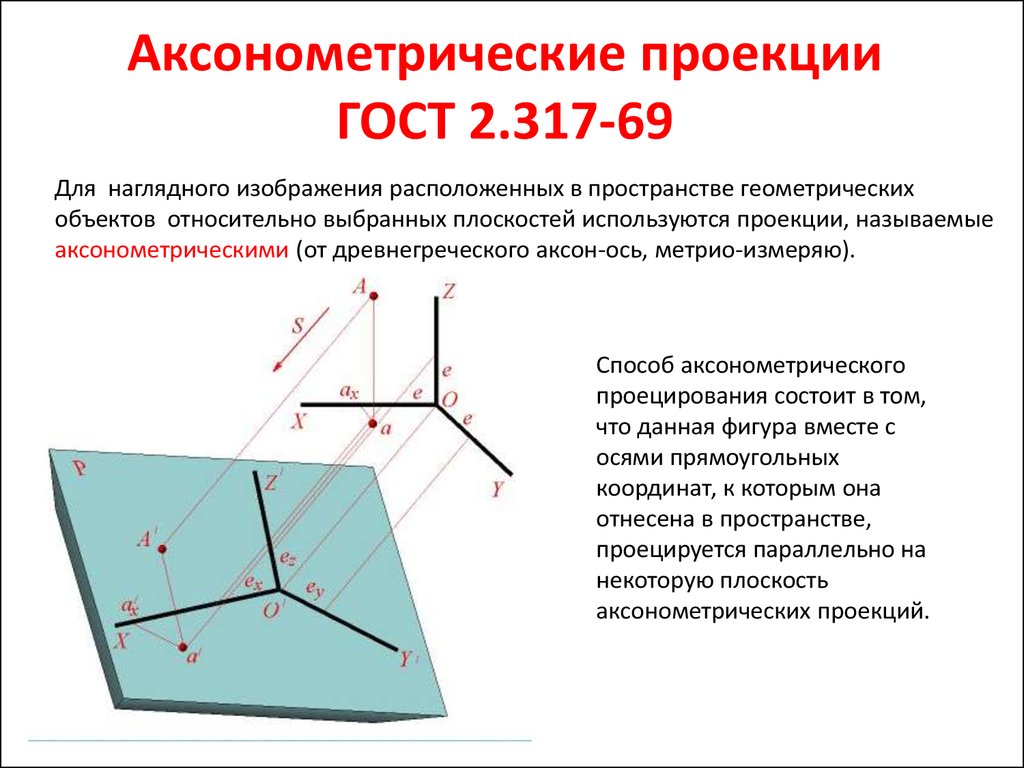 На Рисунке 4.5 большие оси эллипсов 1, 2 и 3 расположены под углом 90º к осям OY, OZ и OX, соответственно.
На Рисунке 4.5 большие оси эллипсов 1, 2 и 3 расположены под углом 90º к осям OY, OZ и OX, соответственно.
Пример прямоугольной диметрической проекции условной детали с вырезом приводится на Рисунке 4.6.
Рисунок 4.5 – Аксонометрические оси в прямоугольной диметрической проекции
Рисунок 4.6 – Изображение детали в прямоугольной диметрической проекции
4.2 Косоугольные проекции
4.2.1 Фронтальная диметрическая проекция
Положение аксонометрических осей приведено на Рисунке 4.7. Допускается применять фронтальные диметрические проекции с углом наклона к оси OY, равным 300 и 600.
Коэффициент искажения по оси OY равен m=0,5 а по осям OX и OZ — k=n=1.
Рисунок 4.7 – Аксонометрические оси в косоугольной фронтальной диметрической проекции
Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на плоскость XOZ без искажения.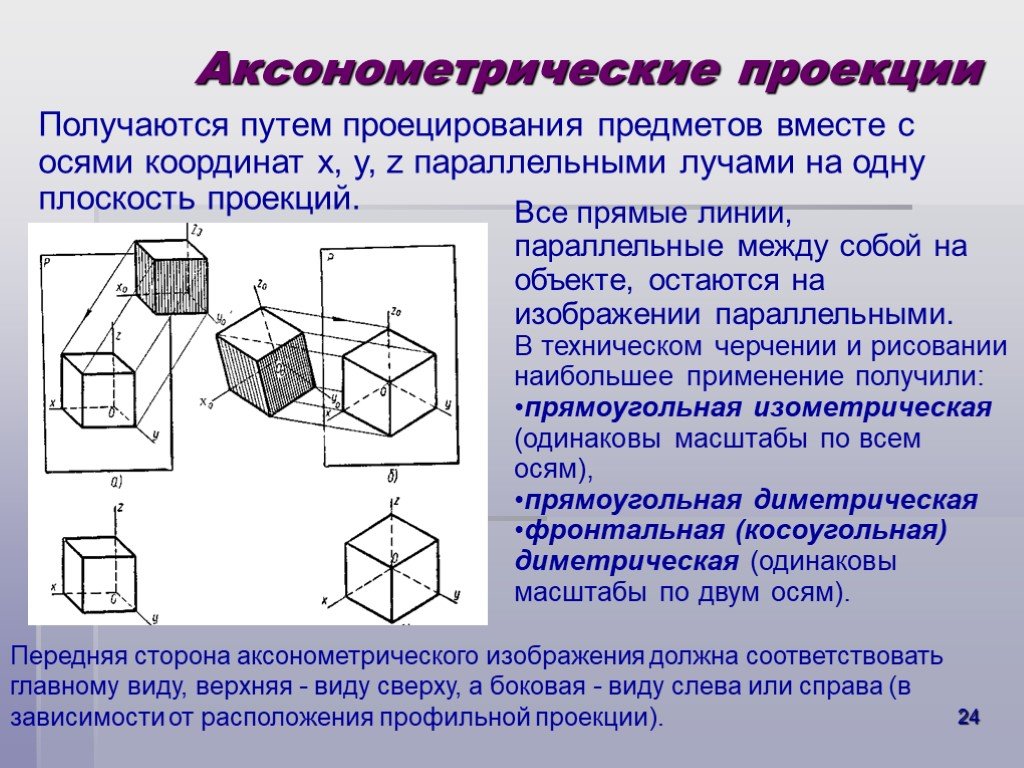 Большие оси эллипсов 2 и 3 равны 1,07D, а малая ось – 0,33D (D — диаметр окружности). Большая ось эллипса 2 составляет с осью ОХ угол 7º 14´, а большая ось эллипса 3 составляет такой же угол с осью OZ.
Большие оси эллипсов 2 и 3 равны 1,07D, а малая ось – 0,33D (D — диаметр окружности). Большая ось эллипса 2 составляет с осью ОХ угол 7º 14´, а большая ось эллипса 3 составляет такой же угол с осью OZ.
Пример аксонометрической проекции условной детали с вырезом приводится на Рисунке 4.8.
Как видно из рисунка, данная деталь располагается таким образом, чтобы её окружности проецировались на плоскость XОZ без искажения.
Рисунок 4.8 – Изображение детали в косоугольной фронтальной диметрической проекции
4.3 Построение эллипса
4.3.1 Построения эллипса по двум осям
На данных осях эллипса АВ и СD строятся как на диаметрах две концентрические окружности (Рисунок 4.9, а).
Одна из этих окружностей делится на несколько равных (или неравных) частей.
Через точки деления и центр эллипса проводятся радиусы, которые делят также вторую окружность. Затем через точки деления большой окружности проводятся прямые, параллельные линии АВ.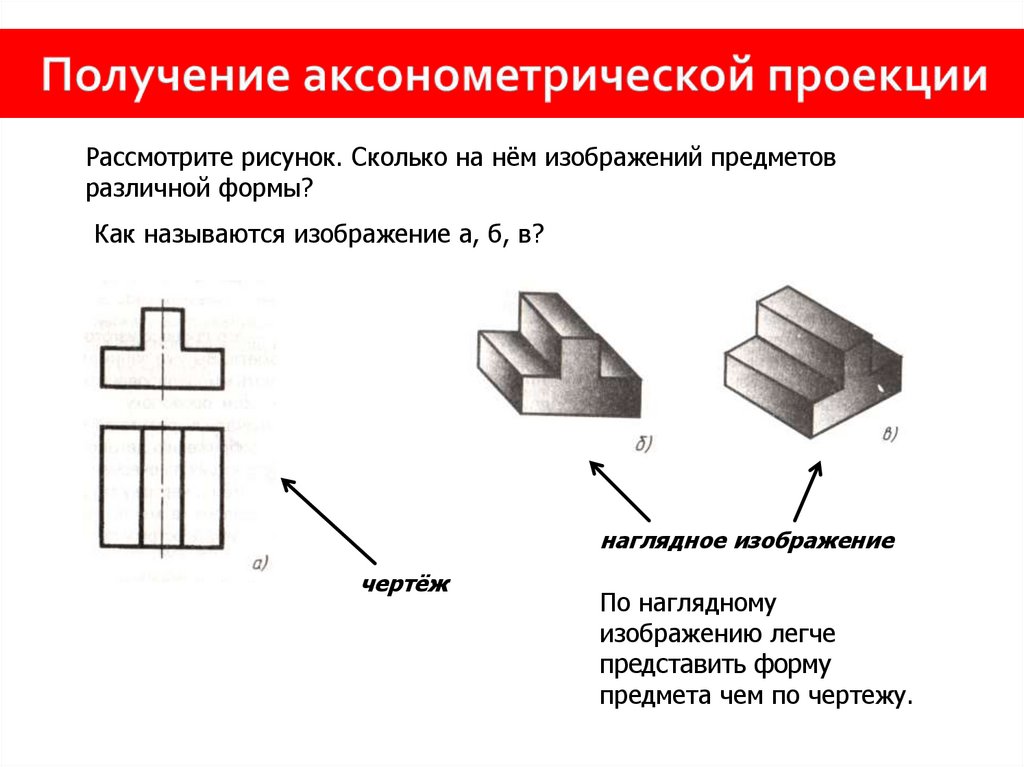
Точки пересечения соответствующих прямых и будут точками, принадлежащими эллипсу. На Рисунке 4.9, а показана лишь одна искомая точка 1.
а б в
Рисунок 4.9 – Построение эллипса по двум осям (а), по хордам (б)
4.3.2 Построение эллипса по хордам
Диаметр окружности АВ делится на несколько равных частей, на рисунке 4.9,б их 4. Через точки 1-3 проводятся хорды параллельно диаметру CD. В любой аксонометрической проекции (например, в косоугольной диметрической) изображаются эти же диаметры с учетом коэффициента искажения. Так на Рисунке 4.9,б А1В1=АВ и С1 D1 = 0,5CD. Диаметр А 1В1 делится на то же число равных частей, что и диаметр АВ, через полученные точки 1-3 проводятся отрезки, равные соответственным хордам, умноженным на коэффициент искажение (в нашем случае – 0,5).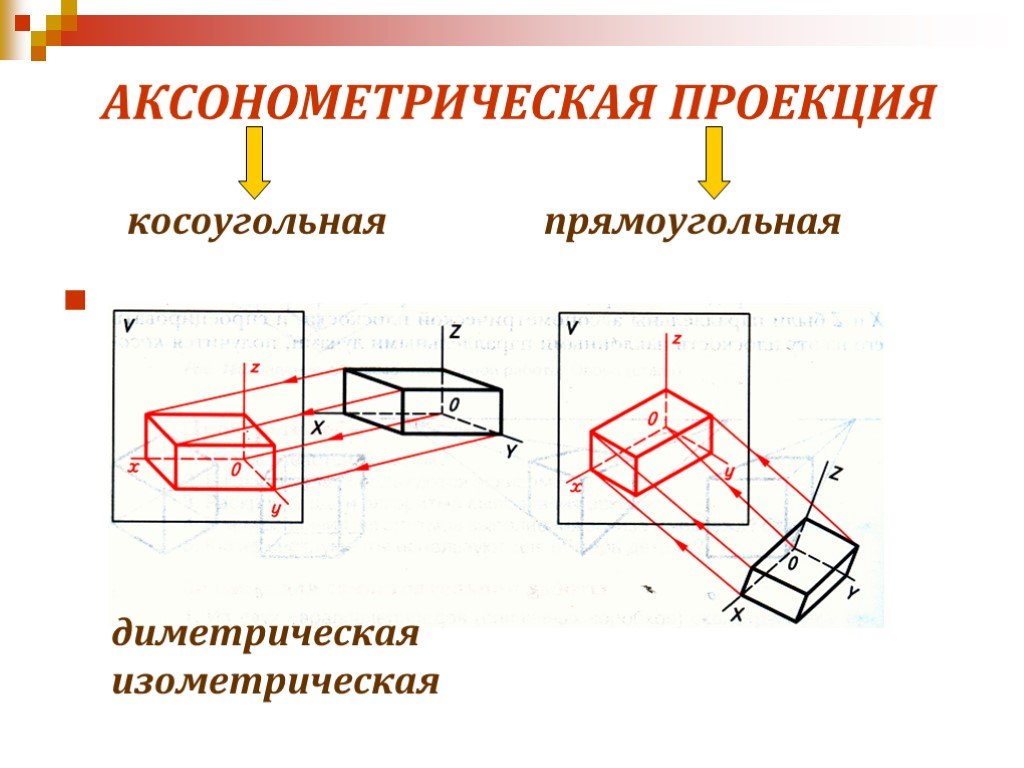
4.4 Штриховка сечений
Линии штриховки сечений (разрезов) в аксонометрических проекциях наносятся параллельно одной из диагоналей квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям (Рисунок 4.10: а – штриховка в прямоугольной изометрии; б – штриховка в косоугольной фронтальной диметрии).
а б
Рисунок 4.10 – Примеры штриховки в аксонометрических проекциях
По вопросам репетиторства по инженерной графике (черчению), вы можете связаться любым удобным для вас способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1250 р./ак.ч.
|
Аксонометрические проекции Категория: Технические чертежи Аксонометрические проекции Параллельным проецированием можно получить наглядные изображения, называемые аксонометрическими проекциями, если расположить изделие определенным образом относительно плоскостей проекций. Аксонометрические проекции — это изображения, полученные путем проецирования параллельными лучами фигуры вместе с осями координат на произвольно расположенную плоскость проекций (аксонометрия измерения по осям). На рис. 31 показано построение прямоугольных (ортогональных) проекций на плоскостях Я и У и аксонометрической проекции на плоскости М0. В качестве предмета взят уголок, жестко связанный с координатными осями х, у, z, параллельными трем измерениям предмета (длине, высоте, ширине). При ортогональном проецировании направление проецирующих лучей выбирают параллельным одной из координатных осей х, у или г. При этом на данной плоскости проекций получают изображение, не дающее пространственного представления о предмете, так как одно измерение предмета, а именно параллельное выбранному направлению проецирования, исчезает. Чтобы получить пространственное представление о предмете в системе ортогональных проекций, необходимо иметь его изображение не менее чем на двух плоскостях проекций; для получения пространственного представления о предмете в системе аксонометрических проекций достаточно получить его изображение на одной, произвольно расположенной плоскости проекций. Рис. 1. Построение проекций уголка. Аксонометрическим проекциям присущи все свойства параллельных проекций. Важнейшие из них следующие: В зависимости от направления проецирующих лучей по отношению к плоскости проекций аксонометрические проекции подразделяются на прямоугольные и косоугольные. Если проецирующие лучи встречают плоскость аксонометрических проекций под прямым углом, то на этой плоскости получаются прямоугольные проекции; если же проецирующие лучи встречают плоскость аксонометрических проекций под углом, отличным от 90°, образуются косоугольные проекции. Показатели искажения по аксонометрическим осям характеризуют изменение размеров аксонометрической проекции предмета в направлении этих осей по отношению к его действительным размерам. Отношения аксонометрических единиц к натуральным называются коэффициентами искажения (показателями искажения) по аксонометрическим осям. Коэффициенты искажения являются отвлеченными числами. Они показывают, в какой пропорции изменяются длины отрезков, взятые на прямоугольных проекциях параллельно той или иной координатной оси, при проецировании их на плоскость аксонометрических проекций. Хотя значения коэффициентов искажения могут быть выбраны произвольно, на практике пользуются теми, которые дают наименьшее искажение изображений предметов. В зависимости от численного значения коэффициентов искажения аксонометрические проекции подразделяются на изометрические, диметрические и триметрические. Проекции, у которых все три коэффициента искажения равны между собой, называются изометрическими, у которых два коэффициента искажения равны — диметричес-кими, и проекции, у которых все три коэффициента искажения имеют разные значения, называют триметрическими. В практике черчения применяются три аксонометрические проекции, дающие наиболее наглядное изображение предмета: прямоугольные, изометрия и диметрия и косоугольная диметрия. Коэффициенты искажения для изометрической проекции по всем трем осям одинаковы и равны 0,82; в прямоугольной диметрии по осям х и z равны 0,94, а по оси у— 0,47; в косоугольной диметрии по осям х и z равны —1, а по оси у — 0,5. При выполнении чертежей принято брать размеры по всем трем осям без искажения, а для диметрической проекции сокращать только по оси у в два раза. В этом случае наглядное изображение получается несколько увеличенным, но наглядность от этого не теряется. Реклама:Читать далее:Фронтальная косоугольная диметрическая проекция
Статьи по теме:
Главная → Справочник → Статьи → Блог → Форум
|
|
|
Архитектурные чертежи: 8 мастерских параллельных проекций
Конкурс One Drawing Challenge теперь является частью предстоящего Награды Architizer Vision Awards , награды за лучшие архитектурные фотографии, рисунки, модели и фильмы за ними стоят талантливые творцы.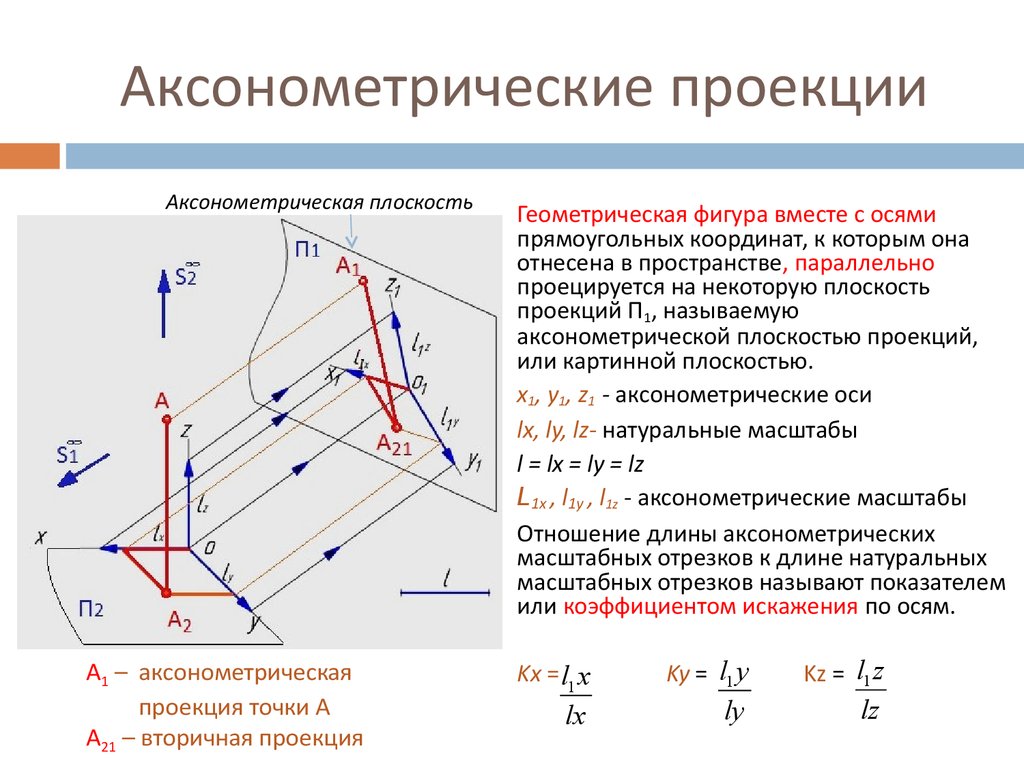 Узнайте больше и зарегистрируйтесь >
Узнайте больше и зарегистрируйтесь >
Аксонометрические чертежи — это мощный инструмент для визуального представления сложных пространственных структур. Их уникальная точка зрения позволяет создавать наглядные рисунки, представляющие трехмерное пространство на двумерной поверхности. При параллельных проекциях обычные законы перспективы не совсем применимы: здесь нет смещения масштаба, как это было бы через объектив камеры или через наши собственные глаза. Хотя эти рисунки часто имеют идеальные пропорции и размеры, они особенно убедительны, поскольку колеблются между реальностью и невозможностью: человеческий глаз никогда не сможет увидеть пространство таким образом.
В этой коллекции рассматриваются несколько применений техники параллельного проецирования, каждый раз используемые художниками и архитекторами для воплощения больших идей. Готовясь к конкурсу One Drawing Challenge, изучите эти увлекательные архитектурные представления и визуализируйте свои собственные… Нью-Йорк
Мастерские ручные рисунки Рудольфа являются свидетельством силы сочетания репрезентативных техник для передачи нескольких аспектов здания.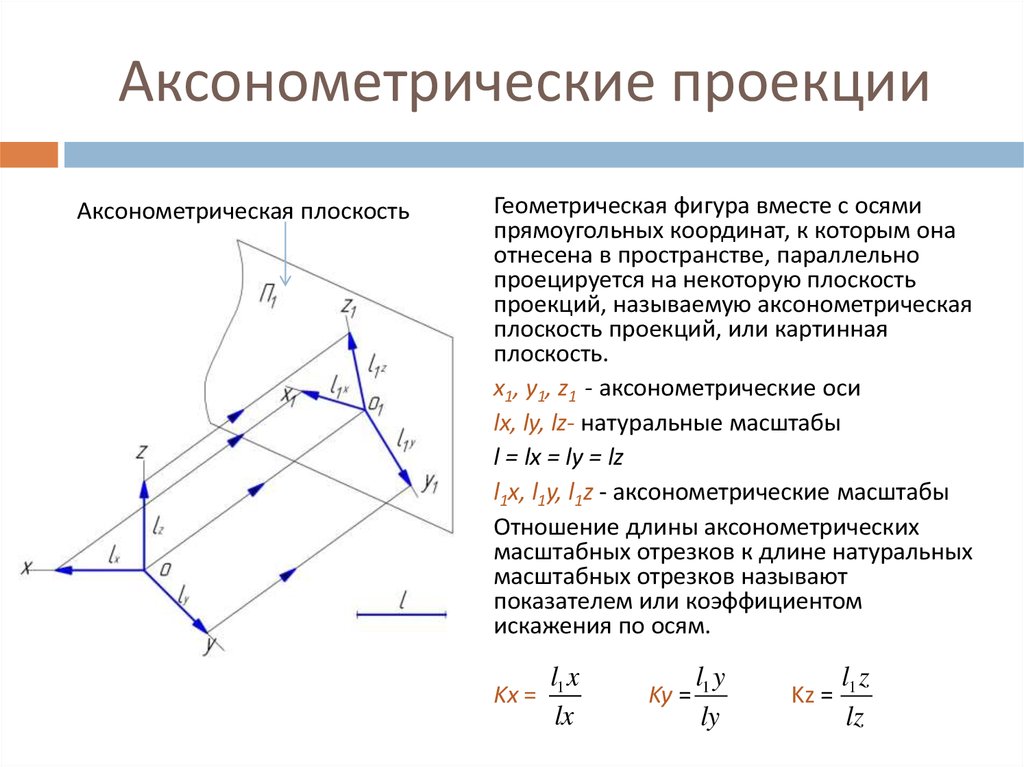 Аксонометрический вид и перспектива сечения работают в тандеме, чтобы передать выступающие прямолинейные объемы внешнего фасада, а также внутреннее пространство внутри них. Две параллельные проекции выше необычны по-разному — первая вращает весь рисунок в пространстве, чтобы обеспечить вид сверху, который представляет здание с правдоподобной точки зрения человека. Второй дает нам вид с высоты птичьего полета, показывая 87 многоуровневых крыш, которые позволяют дневному свету проникать в здание.
Аксонометрический вид и перспектива сечения работают в тандеме, чтобы передать выступающие прямолинейные объемы внешнего фасада, а также внутреннее пространство внутри них. Две параллельные проекции выше необычны по-разному — первая вращает весь рисунок в пространстве, чтобы обеспечить вид сверху, который представляет здание с правдоподобной точки зрения человека. Второй дает нам вид с высоты птичьего полета, показывая 87 многоуровневых крыш, которые позволяют дневному свету проникать в здание.
АЛЬБОМ «Bff016» от SET Architects, Милан, Италия
На этой паре рисунков показано пространство вместе и разорвано. Использование аксонометрической проекции иллюстрирует не только то, как пространство выглядит и может быть заселено, но и абсолютную простоту дизайна. Чертеж разбивает инсталляцию на четыре основных компонента: пол, содержимое, структуру и крышу, демонстрируя модульность и воспроизводимость дизайна.
Изображения через Høyblokka Revisited
Høyblokka Revisited by Kolab Arkitekten + Kollaboratoriet, Осло, Норвегия. рисунки. Благодаря использованию аксонометрического чертежа зритель получает четкое представление о том, как функционируют отдельные блоки в целом жилом комплексе.
рисунки. Благодаря использованию аксонометрического чертежа зритель получает четкое представление о том, как функционируют отдельные блоки в целом жилом комплексе.
Изображения через ArchEyes
Неофутуристические рисунки Яна Каплицкого, Лондон, Великобритания
Эти дальновидные и творческие рисунки являются работой независимой практики Каплицкого Future Systems с 1970-х по 1990-е годы. Он был известен тем, что сказал: «Это не признак творчества — иметь 65 идей для одной проблемы. Это просто пустая трата энергии». Эти детальные рисунки иллюстрируют интерес Каплицкого к упрощению идей в виде уникальных, легко читаемых рисунков. Уникальная точка зрения рисунков позволяет зрителю понять форму и функцию каждого искусно выполненного проекта.
Социально-культурный центр by fala atelier, Reinosa, Испания
Fala atelier, которое игриво описывает себя как «практику наивной архитектуры», производит рисунки, которые обладают уникальным радостным качеством.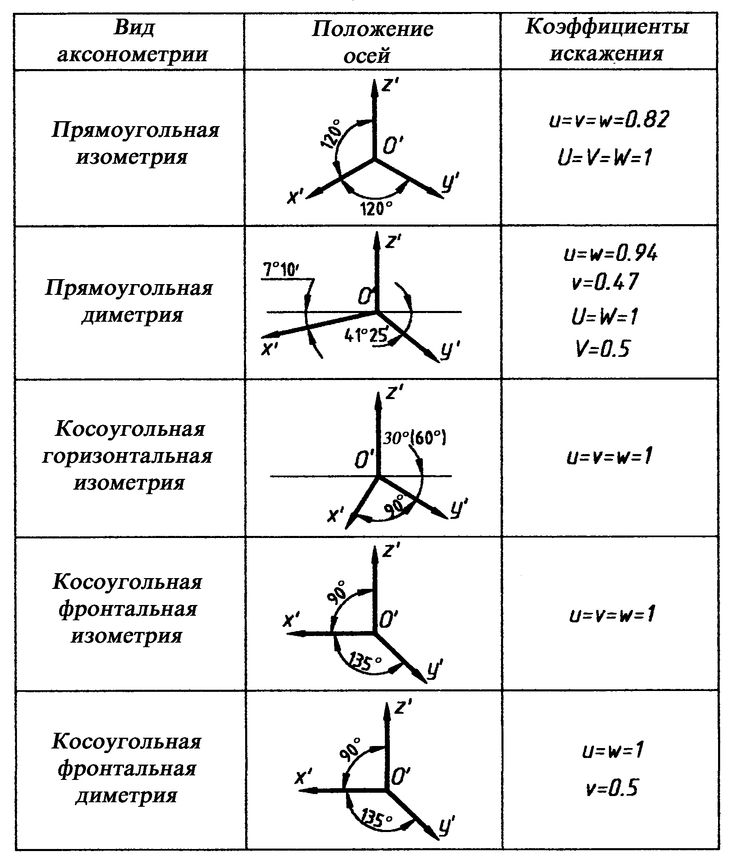 Этот характер пронизывает проекты фирмы от чертежа до реализованного дизайна. Эти рисунки передают основную концепцию проекта с помощью четких линий и продуманных цветовых всплесков. Аксонометрическое представление этого сложного пространства дает ощущение целостности проекта, представляя каждую из 49комнаты как часть более крупной экосистемы.
Этот характер пронизывает проекты фирмы от чертежа до реализованного дизайна. Эти рисунки передают основную концепцию проекта с помощью четких линий и продуманных цветовых всплесков. Аксонометрическое представление этого сложного пространства дает ощущение целостности проекта, представляя каждую из 49комнаты как часть более крупной экосистемы.
© Architecture BRIO
© Architecture BRIO
Дом у ручья и Прибрежный дом от Architecture BRIO, Индия
Река является неотъемлемой частью идентичности обоих этих домов. Архитектура BRIO использует разнесенную аксонометрическую проекцию, чтобы показать каждый дом по отношению к его окружению. В то время как детальная проекция дома парит над землей, включение черного силуэта прямо под ним указывает положение дома в ландшафте. Благодаря использованию разнесенной аксонометрии рисунок успешно предоставляет информацию о самом доме и его положении в ландшафте без ущерба для этого.
Изображения через носки
Ранние коллажи (1967–1970) Даниэля Либескинда
Трудно представить зубчатую скульптурную архитектуру Даниэля Либескинда, когда-либо существовавшую в двухмерной плоскости. Тем не менее, когда Либескинд был студентом Cooper Union в 1960-х годах, его профессора поощряли его исследовать пересечение изобразительного искусства и архитектуры с помощью коллажей и других рисунков.
Тем не менее, когда Либескинд был студентом Cooper Union в 1960-х годах, его профессора поощряли его исследовать пересечение изобразительного искусства и архитектуры с помощью коллажей и других рисунков.
Повернутые на 30 градусов сетки обеспечивают опору для сложной геометрии Либескинда, которая восхищает пространственной неоднозначностью и бросает вызов обычной логике измерения, которую мы ожидаем от аксонометрических проекций. Их смешение создает необычные и очень убедительные работы, которые мастерски стирают грань между искусством и архитектурой.
Tuan Jie Hu от Drawing Architecture Studio, Пекин, Китай
Этот набор чертежей от DAS демонстрирует, что аксонометрические проекции не обязательно связаны с представлением пространств упорядоченным и логическим способом. Эти полуфантастические рисунки окрестностей Пекина используют репрезентативную технику как инструмент, чтобы показать городской динамизм города.
Рисунок следует правилам параллельной проекции, но применяет его к городу с разных точек зрения, создавая нелогичное пространственное расположение. Красочным зданиям, выступающим из сетки в лихорадочном великолепии, удается передать не только реальность застроенной среды, но и нечто большее: уловить феноменологию городской жизни.
Красочным зданиям, выступающим из сетки в лихорадочном великолепии, удается передать не только реальность застроенной среды, но и нечто большее: уловить феноменологию городской жизни.
The One Drawing Challenge теперь является частью предстоящей Architizer Vision Awards , присуждаемой лучшим архитектурным фотографиям, фильмам, визуализациям, чертежам, моделям и талантливым создателям, стоящим за ними. Узнать больше и зарегистрироваться >
Читать другие статьи Orli
Турецкая архитектура отражает контраст между своей сложной историей и современным развитием.
Архитекторы: продемонстрируйте свой следующий проект через Architizer и подпишитесь на нашу inspira
информационный бюллетень.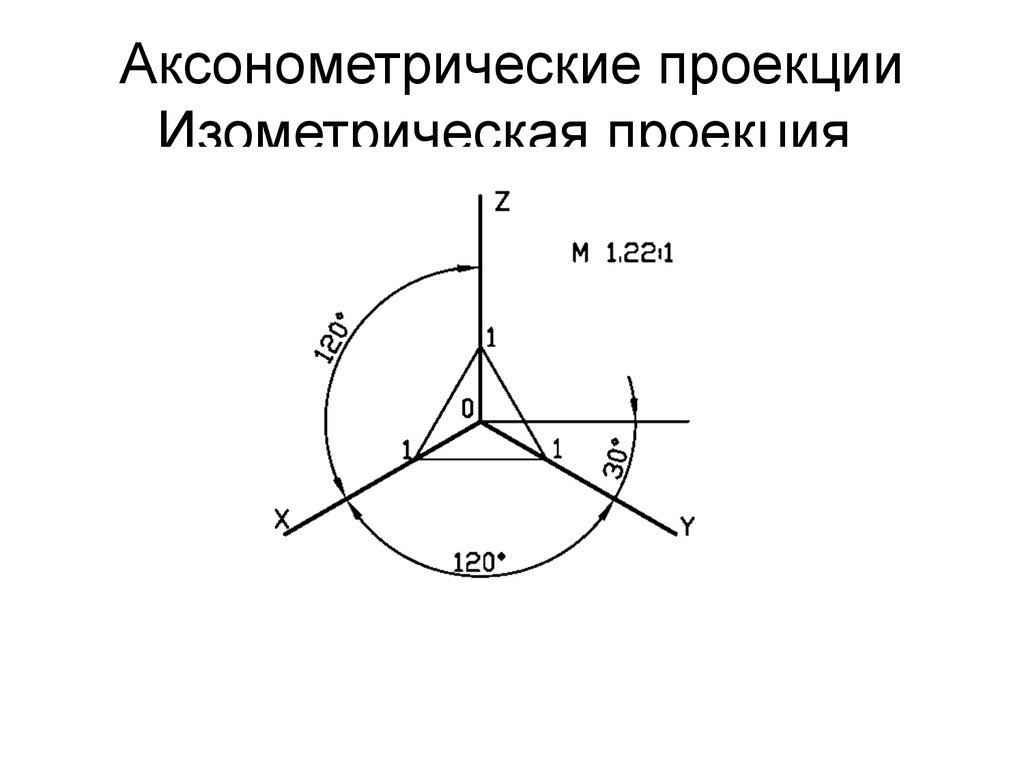 Японский дизайнерский гигант Muji уже давно является пионером простой современной эстетики. Их товары для дома стали синонимом своего рода универсальной, антибрендовой философии, непритязательных, но восхитительных инструментов повседневности. Продукты Muji часто приобретают архетипическое качество, разобравшись до…
Японский дизайнерский гигант Muji уже давно является пионером простой современной эстетики. Их товары для дома стали синонимом своего рода универсальной, антибрендовой философии, непритязательных, но восхитительных инструментов повседневности. Продукты Muji часто приобретают архетипическое качество, разобравшись до…
Аксонометрическое определение и значение — Merriam-Webster
ax·o·не·метрический·метрический
ˌak-sə-nō-me-trik
: быть или подготовлено путем проецирования объектов на поверхность чертежа так, что они кажутся наклонными с тремя видимыми сторонами и с горизонтальными и вертикальными расстояниями, выполненными в масштабе, но с искаженными диагональными и кривыми линиями
аксонометрический чертеж
Примеры предложений
Недавние примеры в Интернете
аксонометрический рендеринг здесь показывает массивные светодиодные экраны в токийском стиле, рекламирующие GeoCities, Lycos и других детей пузыря доткомов, а также прямую трансляцию из зала фондовой биржи молодой Марии Бартиромо.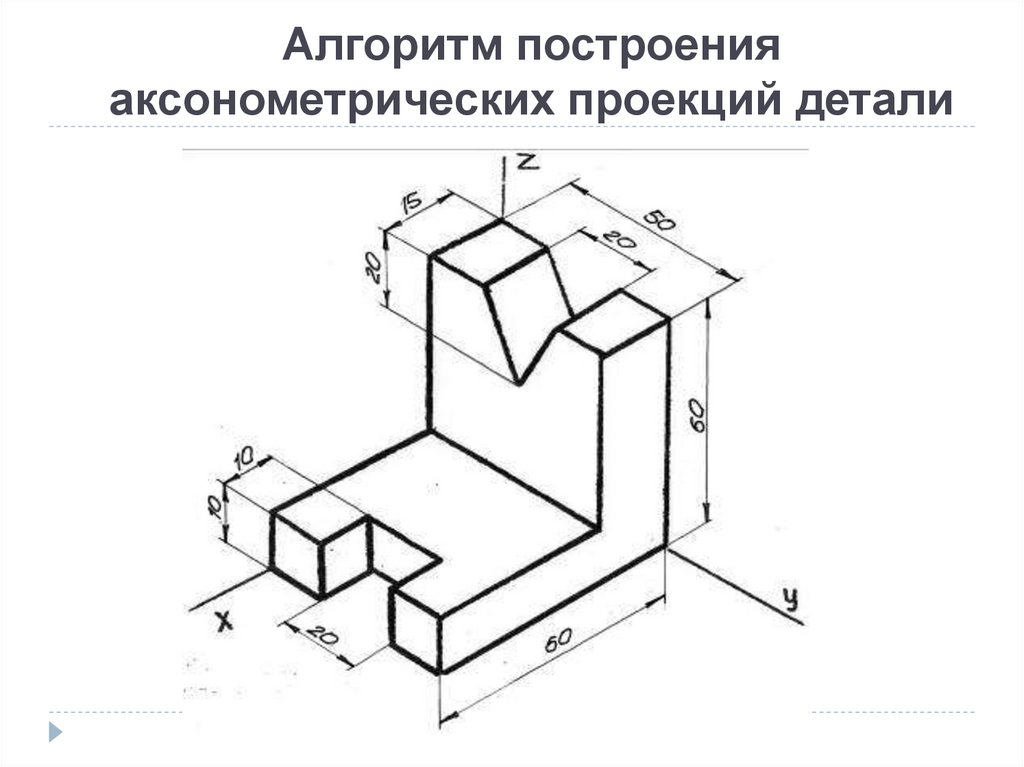
— Джейсон Фараго, New York Times , 11 января 2018 г.
Эти примеры программно скомпилированы из различных онлайн-источников, чтобы проиллюстрировать текущее использование слова «аксонометрический». Любые мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв об этих примерах.
История слов
Этимология
Греческий axōn ось + английский -метрический
Первое известное использование
1869, в значении, определенном выше
Путешественник во времени
Первое известное использование аксонометрических было
в 1869 г.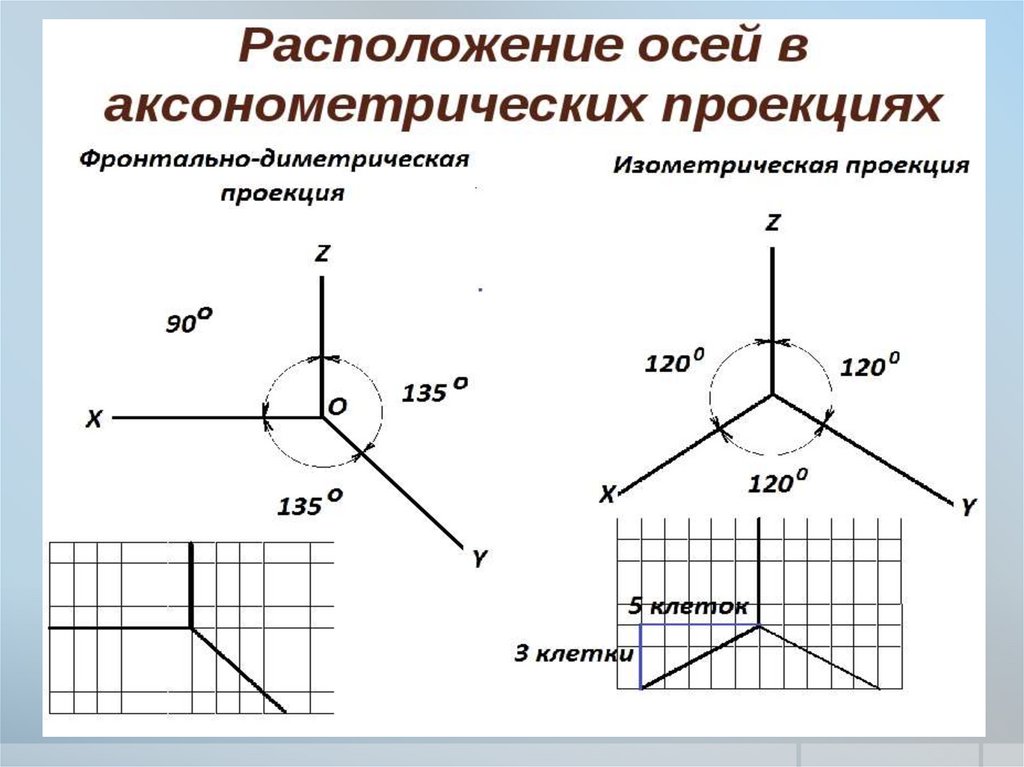
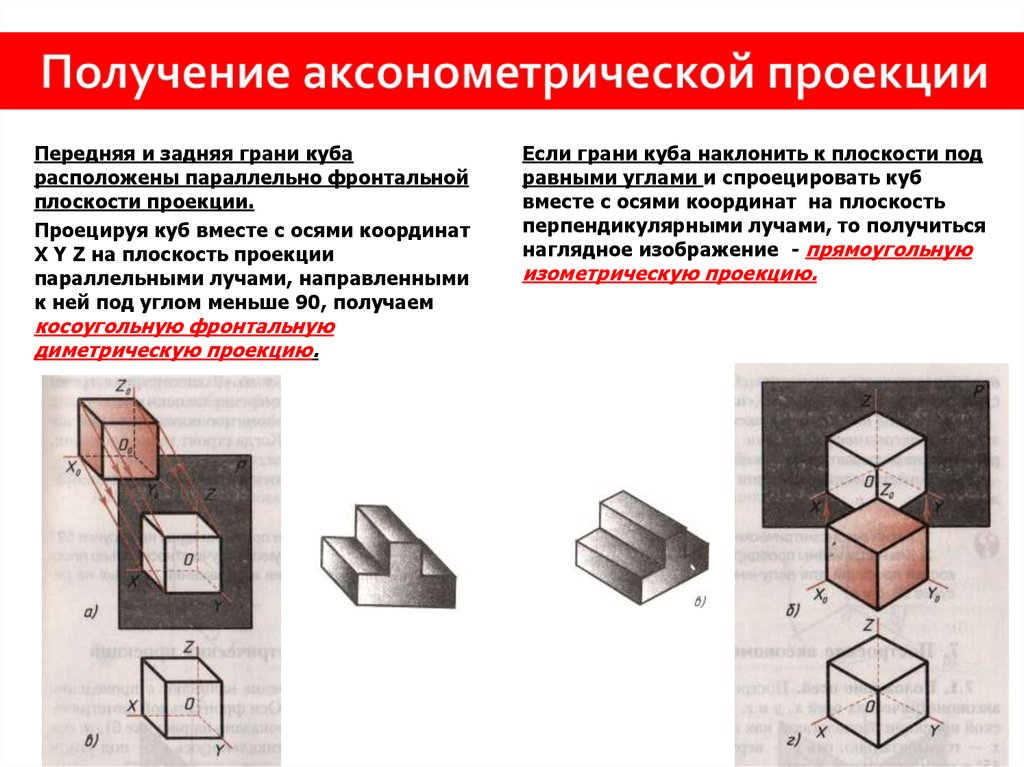
 Для этого необходимо выбрать такое направление проецирования, чтобы оно не совпадало с направлениями координатных осей х, у, z и не было параллельным ни одной из плоскостей проекций Н, V, W (стрелка А). Тогда на некоторой плоскости проекций Мй получается изображение всех трех координатных осей — x:0, y0, z0 (так называемые аксонометрические оси) и изображение трех граней проецируемого предмета (аксонометрическая проекция предмета).
Для этого необходимо выбрать такое направление проецирования, чтобы оно не совпадало с направлениями координатных осей х, у, z и не было параллельным ни одной из плоскостей проекций Н, V, W (стрелка А). Тогда на некоторой плоскости проекций Мй получается изображение всех трех координатных осей — x:0, y0, z0 (так называемые аксонометрические оси) и изображение трех граней проецируемого предмета (аксонометрическая проекция предмета).