Строй-справка.ру. Расчет гибких фундаментов

Проектирование гибких фундаментов

Версия для печати

Задача о распределении контактный напряжений в основании фундаментов сложна как с математической точки зрения, так и с точки зрения ее экспериментальной проверки.

Линейная зависимость распределения напряжений под подошвой фундаментов условная, но она приемлема для расчета жестких фундаментов, так как в этой задаче для учета совместной работы наземной конструкции и сжимаемого основания решающее значение имеют конечные деформации (осадки) основания и возможная предельная нагрузка на основание при данных размерах фундамента в плане.

При расчете фундаментов конечной жесткости (гибких фундаментов-балок и плит) условная линейная эпюра распределения напряжений под подошвой гибкого фундамента неприемлема. Для расчета фундаментов конечной жесткости необходимо учитывать возникающие в конструкциях изгибающие моменты и поперечные силы, которые могут быть подсчитаны после определения эпюры контактных реактивных напряжений по подошве фундамента. Поэтому ошибка в определении последних может привести к значительным погрешностям при определении сечений и процента армирования гибкого фундамента.

Таким образом, при расчете гибких фундаментов необходимо решать задачу о взаимодействии фундаментной конструкции и сжимаемого основания.

Такая постановка задачи требует установления зависимости между реактивным давлением и перемещением основания. Рассмотрим изгиб балки (см. рис.1), нагруженной сосредоточенными силами N1, и N2 , моментами М1 и М2, и распределенной по некоторому закону нагрузкой q = f(х). При этом по подошве балки будет действовать реактивное давление грунта р=f(x), изменяющееся по какому-то сложному закону.

Учитывая, что высота балки намного меньше ее длины и что ее деформации подчиняются закону плоских сечений, по теории сопротивления материалов можно написать дифференциальное уравнение изгиба балки:

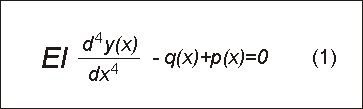
где EI— изгибная жесткость балки; у(х) — некоторая неизвестная функция, выражающая закон прогиба балки в различных сечениях с координатой х.

В этом уравнении имеются две неизвестные функции: одна - уравнение упругой линии у = у(х), вторая — закон распределения реактивных давлений p = р(х).

Решение такой задачи может быть получено лишь при условии написания второго уравнения, в котором будут связаны между собой осадки различных точек балок и реактивное давление.

В зависимости от принятого последнего уравнения применяют тот или иной метод расчета гибких фундаментов. Некоторые из этих методов рассмотрены ниже.

Общая схема расчета гибких фундаментов следующая.

В первую очередь следует установить, к какой категории гибких фундаментов относится данная конструкция, и какая расчетная схема может быть для нее принята.

Гибкие фундаментные конструкции подразделяют на балки и плиты. Балками принято называть конструкции, у которых отношение длины к ширине больше или равно 7; если это отношение меньше, то их называют плитами.

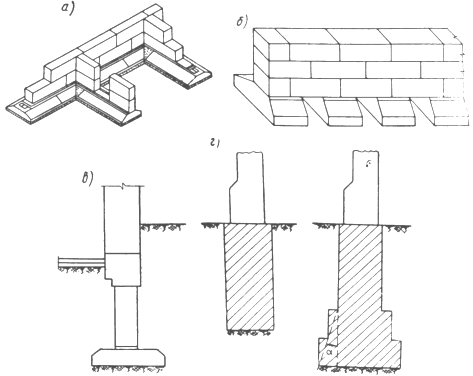
Рис. 2. Схемы работы конструкций:

а — в условиях плоской деформации;

б — в условиях плоского напряженного состояния;

в, г — в условиях осевой симметрии;

д, е — в условиях пространственной задачи

Фундаментные гибкие конструкции могут работать в условиях плоской задачи, пространственной задачи и осевой симметрии.

Конструкции, работающие в условиях плоской задачи, подразделяются на конструкции, работающие в условиях плоской деформации, и на конструкции, работающие в условиях плоского напряженного состояния (см. рис. 2. а, б).

В первом случае выделенный в поперечном направлении любой элемент шириной 1 м работает во всех сечениях одинаково. Поэтому для расчета достаточно выделить один такой элемент. Крайние элементы конструкции будут работать в иных условиях; однако если длина конструкции больше ширины в 3 раза, то ее можно рассчитывать как работающую в условиях плоской деформации. К этой расчетной схеме можно отнести конструкции водосливных плотин, сухих доков, шлюзов, гибких ленточных фундаментов.

В случае плоского напряженного состояния конструкция должна опираться на полуплоскость шириной, равной ширине конструкции. По последней схеме рассчитывают гибкие конструкции типа рандбалок, железобетонных поясов каменных сооружений и т.д.

К конструкциям с осевой симметрией могут быть отнесены круглые гибкие плиты и плиты больших размеров в плане с достаточным удалением нагрузки от края плиты (см. рис. 2. в , г). Круглые плиты с симметричной нагрузкой встречаются при проектировании фундаментов под дымовые трубы котельных, доменных печей, под резервуары и т.д.. По схеме прямоугольных плит с осевой симметрией работают внутренние поля гибких плит, на которые опирается несколько рядов колонн.

Фундаментные конструкции, расчетные схемы которых не подходят под описанные выше, рассчитывают по условиям пространственной задачи. К таким конструкциям относятся многие прямоугольные плиты и балки под колонны, подкрановые пути, железнодорожные шпалы и т.д. (см. рис. 2. д, е).

После уточнения соответствующей расчетной схемы следует определить ориентировочные размеры гибкой конструкции. Размеры конструкции в плане определяют из условия допустимых предельных осадок и краевой критической нагрузки.

Для приближенного определения высоты гибкой конструкции, если она не дана из конструктивных соображений, можно воспользоваться линейной эпюрой распределения давлений под подошвой фундамента. Эпюры поперечных сил и моментов определяют с помощью найденной эпюры реактивных давлений и приложенных внешних сил элементарным путем, как для статически определимой конструкции.

Пример 1. Требуется определить ориентировочную высоту прямоугольной балки, на которую симметрично опираются две колонны. Размеры балки и схема сил показаны на рис. 3, а. Ширина балки b=1 м.

Из условия линейного распределения реактивных давлений грунта получим прямоугольную эпюру контактных напряжений (см. рис. 3, б) с ординатой р, равной:

Имея схему нагрузок и эпюру реактивных давлении, рассчитываем эпюру моментов (см. рис. 3, в). Максимальный момент под силой будет равен:

Из условия максимального момента определим ориентировочную высоту железобетонной балки. Примем бетон марки 200 и процент армирования m = 2,5:

где h0— полезная высота балки, которую можно принять за полную высоту, учитывая относительно большую толщину балки; r — коэффициент, зависящий от процента армирования, марки бетона и типа арматуры; в данных условиях r — 0,173; m — коэффициент условий работы конструкции; примем его равным 1,25.

Рис. 3. Схемы к примеру 1 расчета прямоугольной балки: а — расчетная схема; б — эпюра реактивного давления; в — эпюра моментов.

Найдем толщину балки:

Аналогично определяется ориентировочная толщина плит. Ориентировочное определение размеров гибкой фундаментальной конструкции позволяет перейти к уточнению размеров и процента армирования конструкций. Для этой цели может быть использована достаточно хорошо разработанная теория балок и плит, лежащих на сжимаемом основании.

25 Апреля 2011 г.

gazovik-pgo.ru

Лекция 21. Проектирование гибких фундаментов

Лекция 21.

Проектирование гибких фундаментов При расчете жестких фундаментов была принята линейная зависимость распределений напряжений под подошвой фундамента. При расчете фундаментов конечной жесткости (гибких фундаментов- балок и плит) условная линейная эпюра распределения напряжений под подошвой гибкого фундамента не приемлема. В этом случае необходимо учитывать M и Q, возникающие в самой конструкции фундамента, вследствие действия неравномерных контактных реактивных напряжений по подошве фундамента. Не учет возникающих усилий может привести к неправильному выбору сечения фундамента или % его армирования. Поэтому необходимо решать задачу совместной работы фундаментной конструкции и сжимаемого основания. Какие же фундаменты считать гибкими? Гибкие фундаменты - это те, деформации изгиба которых того же порядка, что и осадки этого же фундамента ∆ S(см) ≈ f(см); ∆ S – осадка фундамента (деформация основания)

f – деформация изгиба фундамента

Таким образом, при расчете гибких фундаментов необходимо одновременно учитывать и деформации фундамента и его осадки.

конструкция грунт

При расчете ленточных фундаментов, загруженных неравномерно сосредоточенными силами - необходимо учитывать изгиб в продольном направлении.

Вследствие изгиба фундамента конечной жесткости давление на грунт увеличивается в местах передачи фундаменту сосредоточенных сил и уменьшается в промежутках между этими силами.

Единого метода расчета гибких фундаментов нет, а существует несколько способов.

Критерий, определяющий состояние фундамента >

- абсолютно жесткие фундаменты

h - гибкие фундаменты

1. Метод прямолинейной эпюры

Области применения:

1 - для предварительных расчетов;

2 - когда не требуется большой точности расчетов;

3 - при слабых сильно сжимаемых грунтах;

Пример:

N1 =N2=80 т

b=1м

Определение ординаты эпюры

контактного напряжения

4. Определяем высоту балки

где

r - коэффициент, зависящий от от % армирования;

m - коэффициент условий работы.

2. Теория местных упругих деформаций. (Гипотеза Фусса-Винклера) 1868г.

Основная предпосылка этой теории – прямая

пропорциональность между давлением и местной осадкой.

; где Px– давление на подошве фундамента

Сz– коэффициент упругости основания

(коэффициент постели)

Zx– упругая осадка грунта в месте приложения

нагрузки

Эта модель хорошо отражает работу конструкции, если основание представлено жидкостью. Поэтому чаще всего этот метод при строительстве на слабых грунтах или в случае малой мощности слоя сжимаемого грунта.

В последнее время было предложено несколько методов, усовершенствующих эту модель: Дутов, Крылов, Кузнецов, Пастернак. Однако модели соответствующие гипотезе Фусса-Винклера не в состоянии учитывать разновидность оснований (изменение Ео по глубине и в плане сооружения).

В действительности эти результаты непосредственных наблюдений показали, что оседает не только нагруженная поверхность, но и соседние участки грунта.

рунт деформируется в соответствии с упругим полупространством. Поэтому была выдвинута другая теория. 3. Теория общих упругих деформаций.

(Гипотеза упругого полупространства)

В основу этой теории положено предположение, что грунт является однородным и изотропным.

Это дало возможность применить к описанию напряженно деформируемого состояния аппарат теории упругости.

Рассмотрим осадку штампа:

Поэтому единого критерия расчета не существует. В каждом конкретном случае необходимо индивидуально подходить к поставленной задачи, оценивая жесткость конструкции и деформируемость основания. И только после этого следует выбирать руководствующую теорию для расчета.

Задачи, рассматриваемые на основании расчета теории балок

или плит на упругом основании.

Плоское напряженное состояние.

(Рассматриваются при опирании конструкции стены. Расчитываются гибкие конструкции типа рандбалок, ж/б поясов).

Плоская деформация.

Бесконечно простирающаяся полоса и нагрузка приложена вдоль всей полосы.

Для расчета необходимо рассматривать единичный элемент.

Рассчитываются гибкие ленточные конструкции - фундамент под стены.

Пространственная задача.

(Трехмерная задача)

(ж/б фундамент под колонну) Расчет балок по методу

местных упругих деформаций ( гипотеза Винклера).

; где

Px– интенсивность давления, передающегося на основание (реактивный отпор грунта в т. Х)

Zx– величина перемещения в т. Х (зависит от жесткости балок, характера распределения нагрузки, размеров балки и деформируемости основания

Сz– коэффициент постели Впервые этот метод был применён при расчете шпал под ж/дор., тогда считали, что Сz= f (грунта), но потом выяснилось, что Сz= f (грунта и ширины подошвы фундамента)

Px=; Сz=; Zx= см

Из сопромата известно уравнение, описывающее изгиб балки:

;

; Значение Рх заменяем исходной формулой:

Решая это уравнение мы найдем Zx: ; А1, А2, А3, А4 - произвольные постоянные, определяемые из

начальных параметров.

В конечном итоге находим Сz и Рх , а следовательно Мх и Qx .

Решение этой задачи во многих случаях приведено в табличной форме в зависимости от конструкции фундаментов (Справочник проектировщика).

;

Расчет балок по методу общих упругих деформаций.

(Гипотеза упругого полупространства) ; где Г - гибкость балки;

l - полудлина балки;

h – высота балки;

Е – модуль упругости материала балки;

Е0 – модуль общей деформации грунта. Г

110 - жёсткая балка (метод Горбунова-Посадова)

Г>10 - гибкая балка Часто при расчете гибких фундаментов (особенно если жесткость балки применима)- переходят к решению задач по методу Жемочкина Б.Н. (Исследование приемов строительной механики для решения статически неопределимых систем). Метод Жемочника для расчета фундаментных балок

на упругом основании. В основу метода положены следующие допущения:

Действительная криволинейная эпюра

распределения давлений под подошвой

балки заменяется ступенчатой

Распределение давлений на ширине балки

также принимаются равномерным.

Между балкой и сжимаемым основанием предполагаются жесткие шарниры опирающиеся стержни, воспринимающие усилия от балки и равномерно распределяющие это усилие на основание.

4. Условие совместимости работы балки и основания и удовлетворяются равенством прогиба балки и осадки основания в месте закрепления опорного стержня yi=Si .

Этот метод является универсальным и позволяет решать любые задачи с любой степенью сложности.

Расчетная схема

Составляется система канонических уравнений (строительная механика):

Задача решается смешанным методом.

- единичное перемещение по направлению "к" связи от воздействия "i" связи

- единичное перемещение, вызванное осадкой основания

- единичное перемещение, вызванное прогибом балки

; -находятся обычно по таблицам

Решив систему уравнений и найдя Xi, определяют величины реактивных давлений Рi, соответствующих ширине принятых участков ступенчатой эпюры (см. допущение № 1):

Затем с использованием метода сечений строят эпюры изгибающих моментов M, а по ним окончательно определяют сечение балки и ее армирование

Область применения: 1. При хороших (плотных) грунтах.

2. Для расчета плит (днища емкостей).

3. При глубоком залегании скалы.1> скачать файл

www.takya.ru

Расчет гибких фундаментов с помощью метода местных деформаций

Навигация:Главная → Все категории → Фундаменты

Расчет гибких фундаментов с помощью метода местных деформаций

Для получения полного решения уравнения (7.6) необходимо к общему решению (7.7) добавить частное решение z, зависящее от нагрузки q0. При условии, если q0 может быть представлена алгебраическим полиномом степени не выше третьей от х, то частное решение может быть найдено с помощью полинома соответствующей степени с помощью метода неопределенных коэффициентов.

Постоянные интегрирования выражения (7.7) определяют из граничных условий.

В общем случае действия на балку различных нагрузок, разбивая балку на определенное количество участков, приходится для каждого из них находить свои значения произвольных постоянных. Это приводит к необходимости для различных, встречающихся на практике, нагрузок составлять и решать большое количество уравнений со многими неизвестными, что существенно усложняет расчет. Однако дальнейшие исследования показали, что в большинстве случаев любую систему нагрузок, приложенных к балке конечной длины, удается заменить системой балок бесконечной длины, прикладывая в их сечениях фиктивные силы и моменты, обеспечивая при этом выполнение граничных условий и заменяя на основании принципа независимости действия сил решение сложной задачи системой простых схем, расчетные усилия для которых известны.

Учет сдвигающих напряжений, вовлекающих в работу ненагруженные зоны грунта рядом с нагруженными, с помощью второго коэффициента постели позволил значительно усовершенствовать метод местных упругих деформаций.

Главное отличие данной модели заключается в том, что основание с двумя коэффициентами постели имеет осадки и за пределами лежащей на нем балки.

Расчет плит с помощью метода местных деформаций значительно сложнее расчета балок.

В настоящее время разработано достаточно большое количество методов расчета, позволяющих получать решение уравнения (7.13) с помощью использования алгебраических полиномов, компенсирующих нагрузок, вариационных методов, конечных элементов и конечных разностей. Разработан целый комплекс программ, дающих возможность проводить расчет плитных фундаментов на ЭВМ с дополнительным учетом касательных напряжений по подошве фундамента, а также жесткости надфундаментных конструкций.

Согласно теории местных упругих деформаций при равномерной нагрузке на балку реакция основания будет одинаковой по всей площади контакта с грунтом, что не подтверждается экспериментальными данными. Аналогичный результат будет получен и при расчете по данному методу жестких фундаментных конструкций.

Еще раз заметим, что метод местных упругих деформаций допускается применять при проектировании гибких фундаментов при наличии в основании слабых грунтов или слоя сжимаемого грунта небольшой мощности.

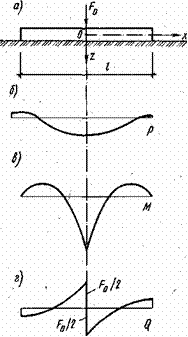
Рис. 7.2. Схема длинной балки, затру- подстилаемого плотным несжиженнои посередвдеойСосредото,енной маемым.

Похожие статьи:Основания под фундаменты зданий и сооружений

Навигация:Главная → Все категории → Фундаменты

Статьи по теме:

Главная → Справочник → Статьи → Блог → Форум

stroy-spravka.ru

Лекция 21. Проектирование гибких фундаментов

Лекция 21.

Проектирование гибких фундаментов

При расчете жестких фундаментов была принята линейная зависимость распределений напряжений под подошвой фундамента. При расчете фундаментов конечной жесткости (гибких фундаментов- балок и плит) условная линейная эпюра распределения напряжений под подошвой гибкого фундамента не приемлема.

В этом случае необходимо учитывать M и Q, возникающие в самой конструкции фундамента, вследствие действия неравномерных контактных реактивных напряжений по подошве фундамента. Не учет возникающих усилий может привести к неправильному выбору сечения фундамента или % его армирования.

Какие же фундаменты считать гибкими?

Гибкие фундаменты - это те, деформации изгиба которых того же порядка, что и осадки этого же фундамента

∆ S(см) ≈ f(см); ∆ S – осадка фундамента (деформация основания)

f – деформация изгиба фундамента

Таким образом, при расчете гибких фундаментов необходимо одновременно учитывать и деформации фундамента и его осадки.^

Единого метода расчета гибких фундаментов нет, а существует несколько способов.

hКритерий, определяющий состояние фундамента> - абсолютно жесткие фундаменты

h - гибкие фундаменты

Области применения:

1 - для предварительных расчетов;

2 - когда не требуется большой точности расчетов;

3 - при слабых сильно сжимаемых грунтах;

Пример:

N1 =N2=80 т

b=1м

Определение ординаты эпюры

контактного напряжения

4. Определяем высоту балки

где

r - коэффициент, зависящий от от % армирования;

m - коэффициент условий работы.

2. Теория местных упругих деформаций.

(Гипотеза Фусса-Винклера) 1868г.

Основная предпосылка этой теории – прямая

пропорциональность между давлением и местной осадкой.

; где Px– давление на подошве фундамента

Сz– коэффициент упругости основания

(коэффициент постели)

Zx– упругая осадка грунта в месте приложения

нагрузки

Грунт деформируется в соответствии с упругим полупространством. Поэтому была выдвинута другая теория.

3. Теория общих упругих деформаций.

(Гипотеза упругого полупространства)

В основу этой теории положено предположение, что грунт является однородным и изотропным.

Это дало возможность применить к описанию напряженно деформируемого состояния аппарат теории упругости.

Задачи, рассматриваемые на основании расчета теории балок

или плит на упругом основании.

Плоское напряженное состояние.

Плоская деформация.

Бесконечно простирающаяся полоса и нагрузка приложена вдоль всей полосы.

Для расчета необходимо рассматривать единичный элемент.

Рассчитываются гибкие ленточные конструкции - фундамент под стены.

(Трехмерная задача)

(ж/б фундамент под колонну)

Расчет балок по методу

местных упругих деформаций ( гипотеза Винклера).

; где

Px– интенсивность давления, передающегося на основание (реактивный отпор грунта в т. Х)

Сz– коэффициент постели

Впервые этот метод был применён при расчете шпал под ж/дор., тогда считали, что Сz= f (грунта), но потом выяснилось, что Сz= f (грунта и ширины подошвы фундамента)

Px=; Сz=; Zx= см

Из сопромата известно уравнение, описывающее изгиб балки:

; ;

Значение Рх заменяем исходной формулой:

Решая это уравнение мы найдем Zx:

; А1, А2, А3, А4 - произвольные постоянные, определяемые из

начальных параметров.

В конечном итоге находим Сz и Рх , а следовательно Мх и Qx .

;

Расчет балок по методу общих упругих деформаций.

(Гипотеза упругого полупространства)

; где Г - гибкость балки;

l - полудлина балки;

h – высота балки;

Е – модуль упругости материала балки;

Е0 – модуль общей деформации грунта.

110 - жёсткая балка (метод Горбунова-Посадова)

Г>10 - гибкая балка

Часто при расчете гибких фундаментов (особенно если жесткость балки применима)- переходят к решению задач по методу Жемочкина Б.Н. (Исследование приемов строительной механики для решения статически неопределимых систем).

Метод Жемочника для расчета фундаментных балок

на упругом основании.

В основу метода положены следующие допущения:

Действительная криволинейная эпюра

распределения давлений под подошвой

балки заменяется ступенчатой

Распределение давлений на ширине балки

также принимаются равномерным.

Между балкой и сжимаемым основанием предполагаются жесткие шарниры опирающиеся стержни, воспринимающие усилия от балки и равномерно распределяющие это усилие на основание.

Этот метод является универсальным и позволяет решать любые задачи с любой степенью сложности.

Расчетная схема

Составляется система канонических уравнений (строительная механика):

Задача решается смешанным методом.

- единичное перемещение по направлению "к" связи от воздействия "i" связи

- единичное перемещение, вызванное осадкой основания

- единичное перемещение, вызванное прогибом балки

; -находятся обычно по таблицам

Область применения:

1. При хороших (плотных) грунтах.

2. Для расчета плит (днища емкостей).

3. При глубоком залегании скалы.1>

velikol.ru

Лекция 21. Проектирование гибких фундаментов

Лекция 21.

Проектирование гибких фундаментов

Какие же фундаменты считать гибкими?

Гибкие фундаменты - это те, деформации изгиба которых того же порядка, что и осадки этого же фундамента

∆ S(см) ≈ f(см); ∆ S – осадка фундамента (деформация основания)

f – деформация изгиба фундамента

Единого метода расчета гибких фундаментов нет, а существует несколько способов.

hКритерий, определяющий состояние фундамента> - абсолютно жесткие фундаменты

h - гибкие фундаменты

Области применения:

1 - для предварительных расчетов;

2 - когда не требуется большой точности расчетов;

3 - при слабых сильно сжимаемых грунтах;

Пример:

N1 =N2=80 т

b=1м

Определение ординаты эпюры

контактного напряжения

4. Определяем высоту балки

где

r - коэффициент, зависящий от от % армирования;

m - коэффициент условий работы.

2. Теория местных упругих деформаций.

(Гипотеза Фусса-Винклера) 1868г.

Основная предпосылка этой теории – прямая

пропорциональность между давлением и местной осадкой.

; где Px– давление на подошве фундамента

Сz– коэффициент упругости основания

(коэффициент постели)

Zx– упругая осадка грунта в месте приложения

нагрузки

Грунт деформируется в соответствии с упругим полупространством. Поэтому была выдвинута другая теория.

3. Теория общих упругих деформаций.

(Гипотеза упругого полупространства)

В основу этой теории положено предположение, что грунт является однородным и изотропным.

Это дало возможность применить к описанию напряженно деформируемого состояния аппарат теории упругости.

Задачи, рассматриваемые на основании расчета теории балок

или плит на упругом основании.

Плоское напряженное состояние.

Плоская деформация.

Бесконечно простирающаяся полоса и нагрузка приложена вдоль всей полосы.

Для расчета необходимо рассматривать единичный элемент.

Рассчитываются гибкие ленточные конструкции - фундамент под стены.

(Трехмерная задача)

(ж/б фундамент под колонну)

Расчет балок по методу

местных упругих деформаций ( гипотеза Винклера).

; где

Px– интенсивность давления, передающегося на основание (реактивный отпор грунта в т. Х)

Сz– коэффициент постели

Px=; Сz=; Zx= см

Из сопромата известно уравнение, описывающее изгиб балки:

; ;

Значение Рх заменяем исходной формулой:

Решая это уравнение мы найдем Zx:

; А1, А2, А3, А4 - произвольные постоянные, определяемые из

начальных параметров.

В конечном итоге находим Сz и Рх , а следовательно Мх и Qx .

;

Расчет балок по методу общих упругих деформаций.

(Гипотеза упругого полупространства)

; где Г - гибкость балки;

l - полудлина балки;

h – высота балки;

Е – модуль упругости материала балки;

Е0 – модуль общей деформации грунта.

110 - жёсткая балка (метод Горбунова-Посадова)

Г>10 - гибкая балка

Метод Жемочника для расчета фундаментных балок

на упругом основании.

В основу метода положены следующие допущения:

Действительная криволинейная эпюра

распределения давлений под подошвой

балки заменяется ступенчатой

Распределение давлений на ширине балки

также принимаются равномерным.

Между балкой и сжимаемым основанием предполагаются жесткие шарниры опирающиеся стержни, воспринимающие усилия от балки и равномерно распределяющие это усилие на основание.

Этот метод является универсальным и позволяет решать любые задачи с любой степенью сложности.

Расчетная схема

Составляется система канонических уравнений (строительная механика):

Задача решается смешанным методом.

- единичное перемещение по направлению "к" связи от воздействия "i" связи

- единичное перемещение, вызванное осадкой основания

- единичное перемещение, вызванное прогибом балки

; -находятся обычно по таблицам

Область применения:

1. При хороших (плотных) грунтах.

2. Для расчета плит (днища емкостей).

3. При глубоком залегании скалы.1>

www.velikol.ru

Лекция 21. Проектирование гибких фундаментов

Лекция 21.

f – деформация изгиба фундамента

конструкция грунт

Единого метода расчета гибких фундаментов нет, а существует несколько способов.

Критерий, определяющий состояние фундамента >

- абсолютно жесткие фундаменты

h - гибкие фундаменты

1. Метод прямолинейной эпюры

Области применения:

1 - для предварительных расчетов;

2 - когда не требуется большой точности расчетов;

3 - при слабых сильно сжимаемых грунтах;

Пример:

N1 =N2=80 т

b=1м

Определение ординаты эпюры

контактного напряжения

4. Определяем высоту балки

где

r - коэффициент, зависящий от от % армирования;

m - коэффициент условий работы.

2. Теория местных упругих деформаций. (Гипотеза Фусса-Винклера) 1868г.

Основная предпосылка этой теории – прямая

пропорциональность между давлением и местной осадкой.

; где Px– давление на подошве фундамента

Сz– коэффициент упругости основания

(коэффициент постели)

Zx– упругая осадка грунта в месте приложения

нагрузки

(Гипотеза упругого полупространства)

В основу этой теории положено предположение, что грунт является однородным и изотропным.

Это дало возможность применить к описанию напряженно деформируемого состояния аппарат теории упругости.

Рассмотрим осадку штампа:

Задачи, рассматриваемые на основании расчета теории балок

или плит на упругом основании.

Плоское напряженное состояние.

Плоская деформация.

Бесконечно простирающаяся полоса и нагрузка приложена вдоль всей полосы.

Для расчета необходимо рассматривать единичный элемент.

Рассчитываются гибкие ленточные конструкции - фундамент под стены.

Пространственная задача.

(Трехмерная задача)

(ж/б фундамент под колонну) Расчет балок по методу

местных упругих деформаций ( гипотеза Винклера).

; где

Px– интенсивность давления, передающегося на основание (реактивный отпор грунта в т. Х)

Px=; Сz=; Zx= см

Из сопромата известно уравнение, описывающее изгиб балки:

;

; Значение Рх заменяем исходной формулой:

Решая это уравнение мы найдем Zx: ; А1, А2, А3, А4 - произвольные постоянные, определяемые из

начальных параметров.

В конечном итоге находим Сz и Рх , а следовательно Мх и Qx .

;

Расчет балок по методу общих упругих деформаций.

(Гипотеза упругого полупространства) ; где Г - гибкость балки;

l - полудлина балки;

h – высота балки;

Е – модуль упругости материала балки;

Е0 – модуль общей деформации грунта. Г

110 - жёсткая балка (метод Горбунова-Посадова)

на упругом основании. В основу метода положены следующие допущения:

Действительная криволинейная эпюра

распределения давлений под подошвой

балки заменяется ступенчатой

Распределение давлений на ширине балки

также принимаются равномерным.

Между балкой и сжимаемым основанием предполагаются жесткие шарниры опирающиеся стержни, воспринимающие усилия от балки и равномерно распределяющие это усилие на основание.

Этот метод является универсальным и позволяет решать любые задачи с любой степенью сложности.

Расчетная схема

Составляется система канонических уравнений (строительная механика):

Задача решается смешанным методом.

- единичное перемещение по направлению "к" связи от воздействия "i" связи

- единичное перемещение, вызванное осадкой основания

- единичное перемещение, вызванное прогибом балки

; -находятся обычно по таблицам

Область применения: 1. При хороших (плотных) грунтах.

2. Для расчета плит (днища емкостей).

3. При глубоком залегании скалы.1> скачать файл

takya.ru

Теории изгиба балок и плит на упругом основании и условия их применимости к расчету гибких фундаментов

Навигация:Главная → Все категории → Фундаменты

Теории изгиба балок и плит на упругом основании и условия их применимости к расчету гибких фундаментов

Для гибких фундаментов, которые в основном воспринимают изгибающие моменты, образующиеся в результате совместной работы с основанием, предположение о линейном распределении реактивных давлений оказывается неприемлемым, потому что оно зависит от жесткости фундамента и податливости грунтового основания.

Замена реальной эпюры контактных давлений линейно распределенной приводит к существенным погрешностям при определении изгибающих моментов и поперечных сил.

К гибким фундаментам можно отнести ленточные и отдельные железобетонные фундаменты, а также сплошные железобетонные плиты и некоторые типы коробчатых фундаментов.

В зависимости от вида используемого фундамента различают плоскую задачу, когда условия работы поперечного сечения фундамента одинаковы по длине. Например, ленточный фундамент под стену в поперечном сечении имеет одинаковую форму деформации по всей длине.

В условиях пространственной задачи будут находиться ленточный фундамент под колонны, принимаемый в поперечном направлении жестким, и фундаментные плиты различной формы, работающие на изгиб в двух направлениях.

В настоящее время большое распространение при проектировании гибких фундаментов получили теории расчета балок и плит на упругом основании, которые справедливы для линейно деформируемых оснований, причем наибольшее применение получили следующие методы: 1) местных деформаций с постоянным и переменными коэффициентами постели; 2) упругого полупространства; 3) упругого слоя ограниченной толщины на несжимаемом основании; 4) упругого слоя с переменным модулем деформации основания по глубине.

Эти теории исходят из предположения о совместности деформации, фундамента и грунта, т. е. считается, что перемещение фундамента в данной точке контакта равно осадке поверхности грунта.

В методе местных упругих деформаций не учитываются осадки грунта основания за пределами площади загружения, что дает возможность представить такое основание в виде системы несвязанных между собой упругих пружин (рис. 7.1, а). Такие условия работы грунтового основания не подтверждаются экспериментальными данными, которые показывают, что в реальных условиях нагружения оседают не только нагруженная поверхность, но и соседние участки грунта (рис. 7.1, б). Это ограничивает область применения данного метода на практике.

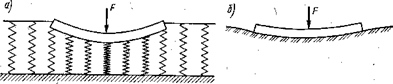
Рис. 7.1. Схемы упругого основания

Метод местных упругих деформаций используют для слабых грунтов основания, для которых можно не учитывать осадки вне зоны приложения внешней нагрузки или в случае незначительной мощности деформируемого грунта, подстилаемого скальным основанием при полупролет рассчитываемого фундамента.

С целью расширения области применения данного метода для расчета гибких фундаментов стали учитывать переменное значение коэффициента постели по длине балки в зависимости от уровня действующего реактивного давления.

Метод упругого полупространства не имеет недостатков, присущих методу местных деформаций, так как он базируется на решениях классической теории упругости, рассматривающей однородные, упругие линейно деформируемые тела.

В соответствии с этими решениями осадки основания имеют место не только на участке под гибким фундаментом, но и за его пределами (рис. 7.1, б).

Однако и метод расчета гибких фундаментов при моделировании грунтового основания упругим полупространством не свободен от некоторых недостатков. В частности, экспериментальными исследованиями было доказано, что осадки за пределами площади загружения затухают значительно быстрее, чем это происходит согласно решению задачи деформирования упругого полупространства. Это связано с тем, что исходные предпосылки теории упругости могут быть применимы к грунтам только с. некоторыми ограничениями, допускающими некоторую идеализацию реальных свойств.

Наблюдения за деформациями оснований гибких фундаментов показали, что основные деформации уплотнения грунта происходят в пределах относительно небольшой глубины. Анализ результатов таких наблюдений показал, что поверхность грунта под возводимыми зданиями и гибкими фундаментами деформируется в соответствии с расчетной схемой линейно деформируемого слоя грунта, подстилаемого несжимаемым основанием.

Основная трудность при использовании этого метода заключается в том, что не всегда точно удается установить мощность сжимаемого слоя.

Похожие статьи:Основания под фундаменты зданий и сооружений

Навигация:Главная → Все категории → Фундаменты