Архитектура в золотом сечении: Золотое сечение в архитектуре — Информио

Золотое сечение в архитектуре — Информио

Феномен золотого сечения известен человечеству очень давно. Его тайну пытались осмыслить многие крупнейшие мыслители человечества: Евклид, Платон, Леонардо да Винчи, Кеплер и другие. Они неразрывно связывали золотое сечение с понятием всеобщей гармонии, пронизывающей вселенную. Классическими проявлениями золотого сечения являются предметы обихода, скульптура, архитектура, математика. Мы довольно часто в повседневной жизни встречаемся с таким понятием как красота архитектурного сооружения. И часто с таким понятием совмещаем пропорциональность, то есть употребляем такой термин: «В архитектуре этого здания не выдержаны пропорции» [4].

На этой пропорции базируются основные геометрические фигуры. Например, прямоугольник, в котором отношение большей части к меньшей равно пропорции золотого сечения. Или золотой треугольник, который представляет собой равнобедренный треугольник, у которого отношение длины боковой стороны к длине основания равняется 1. 618.

Классическими проявлениями данного феномена служат предметы обихода, архитектура, скульптура, музыка, математика и эстетика. В прошлом столетии с расширением области человеческих знаний резко увеличилась численность сфер, где есть феномен золотого сечения. Это зоология, биология, экономика, кибернетика, психология, астрономия, геология и теория сложных систем [5].

Золотое сечение – это пропорциональное деление отрезка на неравные части, при котором меньший отрезок так относится к большему, как больший ко всему. Принято считать, что понятие о золотом сечении ввёл в научный обиход Пифагор [3].

В архитектуре, как и в живописи, всё зависит от положения наблюдателя, и что, если некоторые пропорции в здании с одной стороны кажутся образующими золотое сечение, то с других точек зрения они будут выглядеть иначе. Золотое сечение даёт наиболее спокойное соотношение размеров тех иных длин [8]. Древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзье нашел, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления [1].

Золотое сечение – это гармоническая пропорция [3]. Под ним понимается такая пропорция, которой в древности приписывали необычные свойства. Если разделить объект на две неравные части таким образом, что отношение меньшей к большей будет таким же, как отношение большей ко всему объекту, тогда мы и получим золотое сечение в архитектуре.

Такое соотношение упрощенно можно представить, как два к трем или три к пяти. Уже давно было установлено, что людьми объекты, содержащие золотое сечение, воспринимаются, как наиболее гармоничные, то есть красивые и приятные для глаз.

В книгах об этом феномене встречаются заметки о том, что в плане архитектуры все зависит от того, в каком положении находится наблюдатель, поэтому, если какие-то пропорции здания с одного ракурса кажутся формирующими золотое сечение, при этом с другой стороны они могут выглядеть совсем иначе [5].

Золотое сечение в архитектуре замечено давно. Можно указать такие объекты, как египетские пирамиды, а также многие произведения искусства — скульптуры, картины и кинофильмы. Для большинства использование золотого сечения является интуитивным. Однако некоторые это делали сознательно [5].

Историки искусства находили пропорции близкие к золотому сечению, в архитектурной древности начиная с Египетских пирамид. Наиболее же известным и ярким примером применения золотого сечения в античной архитектуре является, пожалуй, Парфенон. Он был построен в 447 – 438 годах до н. э. архитектором Калликратом по проекту Иктина и украшен в 438 – 431 годах до н. э. под руководством Фидия. Золотое сечение легко угадывается в пропорциях Парфенона [6].

Читать работу полностью (оригинал работы):

Золотое сечение в архитектуре

Примеры золотого сечения в архитектуре, его применение

Примеры золотого сечения в архитектуре найти можно везде, когда умеешь его видеть. Выяснить это даже школьнику по силам. В 2013 году ученица 10 класса Сивакова Елена провела собственное исследование зданий 19-20 веков. Проследим, как она это сделала, и научимся видеть и определять его в архитектурных сооружениях за 5 минут. После прочтения статьи не останется вопросов о том, что это такое, и можно ли его необычные свойства использовать в своей жизни.

Содержание

7+ примеров золотого сечения в архитектуре России

Санкт-Петербург

Здания исторического центра Санкт-Петербурга построены в разных архитектурных стилях, таких как барокко, классицизм, ампир, эклектика, необарокко, неоготика.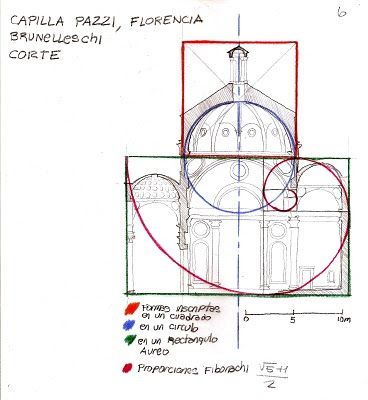 Подчиняются ли они золотому правилу?

Исаакиевский собор

Придворный архитектор Александра I Огюст Монферран строил этот собор с 1819 по 1858 гг. Стиль позднего классицизма, в котором уже проявлены черты неоренессанса и эклектики. Елена задалась вопросом: «В чём же причина гармонии довольно громоздкого здания?»

Свой поиск она начала, как рекомендуется в методике профессора Московского архитектурного института Ю.Н.Герасимова, с фасада собора. На чертеже просматриваются три ряда Золотого сечения.

Первый ряд определён шириной здания, которая принята за 400 ед. и представляет такие цифры 400, 247, 153, 94, 58…

Если 400 разделим на число ≈1,618, то получим приблизительно 247; повторяем действие со следующим числом: 247: 1.618≈153.

И так находим все числа. Теперь смотрим на рисунок. Основная часть с колоннами вписывается в прямоугольник со сторонами 400 и 247. Поскольку стороны находятся в соотношении Ф≈1.618, то они образуют Золотой прямоугольник.

Следующий ряд представлен высотой здания: 370, 228, 140, 87, 53, 33, 20, 12. Эти размеры заложены в более мелкие детали. По вертикали Исаакиевский собор делится Золотым сечением у основания купола, что делает соотношение основной части и купола гармоничным.

Третий ряд размеров начинается со 113, и являет ширину основания главного купола: 113, 69, 42, 26, 16. Числа этого ряда встречаются в размерах окон, в высотах колонн и других деталей собора.

Золотые прямоугольный и равнобедренный треугольники имеют место в здании Исаакиевского собора, как видно из рисунка.

Кунсткамера

На Университетской набережной Васильевского острова стоит здание Кунсткамеры, заложенное в 1718 году под руководством немецкого архитектора Георга Маттарнови: Петровское барокко, два 3-этажных корпуса и сложная многоярусная купольная башня.

Исследование начинается с главных величин: высоты и длины здания, от которых строится золотой ряд. Длина — 450 ед., далее 277, 170, 105, 65, 40, 24. Такие размеры можно видеть в высоте и широте разных уровней башни, длине корпусов. Сама башенная часть вписана в золотой равнобедренный треугольник от основания до вершины. Золотое сечение просматривается в большей степени именно в этом главном элементе, что правильно с точки зрения архитектуры. Вывод: основа Кунсткамеры подчиняется золотому правилу и сохраняет композиционную гармоничность.

Новый золотой ряд начинает высота здания: 211, 130, 80, 49, 30. Глядя на размеры чертежа, становиться понятно, что выбор трёхэтажного вида корпусов обусловлен соразмерностью с башней.

Торговый дом «Эсдерс и Схейфальс» на пересечении Мойки и Гороховой

Построено в 1907 году по проекту Владимира Александровича Липского и Константина Николаевича де Рошефора (Рошфора). В 1905 г. бельгиец С. Эсдерс и нидерландец Н. Схейфальс подали прошение о разрешении построить пятиэтажное здание с куполом и шпилем на угловой башне для их торгового дома вместо старого.

С длины здания в 671 ед. начинается ряд Золотого сечения, наблюдаемого в размерах: 671, 414, 256, 158, 98, 60, 37, 23.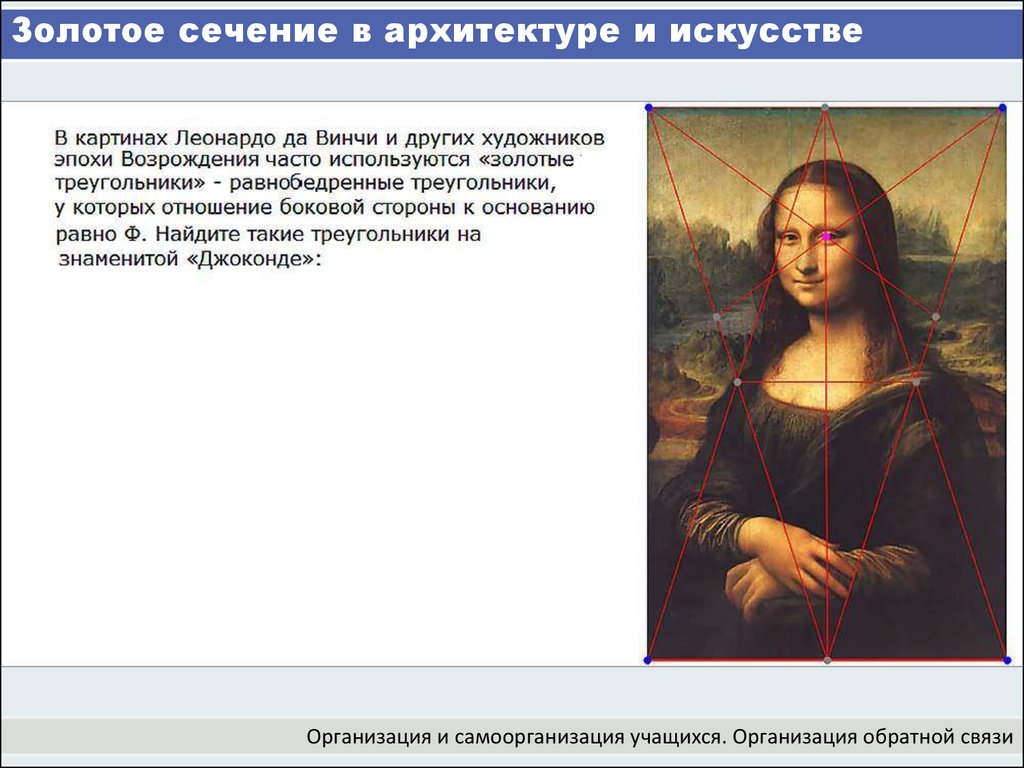 Обращаем внимание на основной элемент — шпиль. Убеждаемся, что композиционное решение завершено гармоничным сочетанием высотных величин.

Дом Советов на Московской площади

Построен в 1941г по проекту Ноя Абрамовича Троцкого. Здание советского периода рассматривают как творческую интерпретацию классики. Центральный портик с четырнадцатью колоннами завершает скульптурный ансамбль на тему строительства социализма и гербом Российской Советской Федеративной Социалистической Республики.

По бокам симметрично расположены пятиэтажные корпуса. Длина Дома достигает 1472 ед., из которого методом деления на число Ф получается ряд размеров элементов здания: 1472, 909, 562, 34, 214, 132, 81, 50 (Приложение 21): высоты сооружения, высоты входа и др.

Вершина Золотого равнобедренного треугольника совпадает с вершиной здания, а его стороны проходят через вехние точки главного входа. Прямоугольный золотой треугольник образован вершинами в верхушке здания и в конце внутренней части бокового крыла. Пропорциональность очевидна, хотя и не имеет большой композиционной значимости.

Москва

Московский Государственный Университет на Воробьёвых горах

Над его проектом работал коллектив под управлением Б.М.Иофана, которого позже сместили с должности главного архитектора. Образец послевоенной советской архитектуры выстроен с 1949 по 1953 годы.

Б.М.Иофан предложил композицию из пяти составляющих с центральной башней. В годы строительства это было самое высокое здание в Европе.

Длина здания равна 1472 ед. и начинает ряд: 909, 562, 347, 214, 132, 81, 50. Золотому сечению подчиняются, в основном высотные размеры. Из ширины башни проистекает другой ряд: 538, 332, 205, 126, который видим в широтных размерах.

Золотой прямоугольный треугольник гипотенузой проходит через угол здания и захватывает пристройки.

Таким образом, во всех исследуемых зданиях ученица обнаружила Золотое сечение, сохраняющее гармонию.

5 примеров дополнительно

Чтобы упростить задачу поиска ЗС, можно брать рациональные дроби 3/2; 5/3; 8/5; 13/8; 21/13; 34/21; 55/34; 89/55; и так дальше.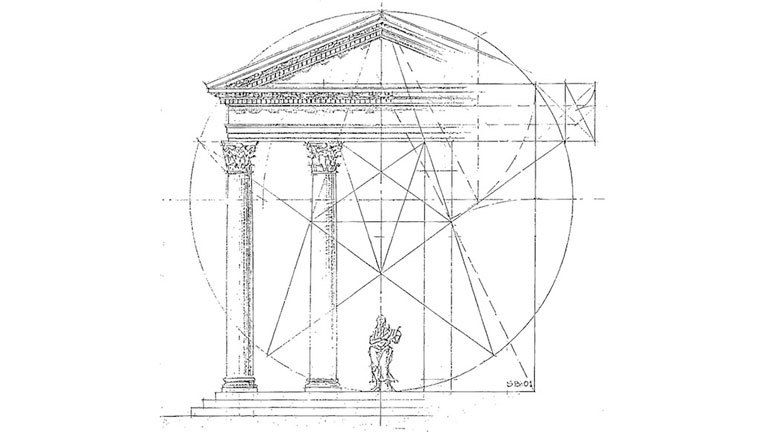 Закономерность ясна: 3+2 =5; 5+3=8; 8+5=13… Или ещё проще. Сделайте себе циркуль для определения пропорции по инструкции в видео. Времени уйдет минут 10. Как пользоваться этим циркулем для определения пропорциональности элементов тоже расскажут и покажут.

Применяя этот способ, находим золотую пропорцию русского зодчего Матвея Казакова в кремлёвском здании сената, да и во всех остальных работах: Пречистенском дворце в Москве, Благородном собрании, Голицынской больнице (им. Пирогова)…

Созданный другим великим архитектором Василием Ивановичем Баженовым дом Пашкова в Москве (Российская государственная библиотека) причисляют к образцам совершенных архитектурных памятников, в котором легко определить ЗС.

Ужасный символ Парижа и золотое сечение

Когда в Париже собирали металлическую Эйфелеву башню, многие французы возмущались. Критики писали о ней, как об «уродстве города», «сраме Парижа», «тощей пирамиде из металлических лестниц». В их числе были Эмиль Золя, Дюма-младший, Ги де Мопассан. Сейчас этот самый посещаемый памятник является гордостью парижан. Может быть виной тому «божественная» пропорция?

Она же наблюдается и самом знаменитом французском соборе Нотр-Дам-Де-Пари.

Вся правда о древних строителях

Интуитивно или сознательно великие архитекторы строили здания с учётом этих пропорций? Античные математики знали о золотом сечении со времён Пифагора. Находятся всё новые подтверждения его применения в архитектурных пропорциях. Однако не найти ни одной древней записи с прямой рекомендацией использовать “божественную пропорцию”. Нет таковой и у Витрувия (I век до н. э.), написавшего «Десять книг об архитектуре», в которых он рассматривал пропорциональности в том числе. Странный факт, не правда ли?

Может все выше приведённые исследования являются подгонкой под известный результат? Не так сложно выбрать из множества архитектурных элементов те, которые подтверждают гипотезу, т.  к. абсолютной точности никто не требует. Логично задуматься над вопросом: «Что если греки НЕ применяли золотое сечение?»

Собственно говоря, и для Луки Пачоли, написавшего в 1509 году труд «Божественная пропорция», не столь важно было его прикладное значение. Важно было обосновать её мистическую природу. А применять его осознанно стали только с момента издания книги.

Тайна архитектуры Древней Греции

Красивые и гармоничные объекты всегда отвечают правилу ЗС, а при анализе величин определяется эта пропорциональность. Искусствоведы внимательно изучили греческий Парфенон, возведённый в честь победы над персами — храм богини Афины. Отношение длины храма к ширине даёт золотое число с маленькой погрешностью. Если отнять от длины сооружения 14 см и прибавить к ширине, то получится полное совпадение с математической величиной. Фасад здания немного сужается кверху, отклоняется от прямоугольной формы. Учитывая визуальное восприятие, сделано это строителями сознательно. Поэтому считать его прямоугольником золотого сечения не совсем корректно. Но пропорции соблюдаются, так что логично предположить, что архитекторы Иктин и Калликрат умышленно заложили правило в проект?

Мифы и диковинные факты о пирамиде

Пирамида Хеопса также выстроена с учётом этого условия. Не вдаваясь в математическое доказательство наличия золотой формулы, скажем только, что в нём присутствуют прямоугольный золотой треугольник, сторонами которого являются высота и половина стороны основания строения. Ничего удивительного?

Но тогда возникает вопрос об уровне древнеегипетской математики. Выходит, что теорема Пифагора была им известна за два тысячелетия до рождения самого учёного. Внимание привлекает факт, что наследники Хеопса строили свои пирамиды уже с другими пропорциями. Почему?

Установлено, что сооружения пирамидальной формы с ЗС оказывают на находящихся в них феноменальное воздействие: растения лучше растут, металлы становятся прочнее, вода долго остаётся свежей. Учёные много лет работают с этими загадками, но тайна остаётся.

Замечено, что пирамида приводит структуру пространства в слаженное состояние. Всё, что попадает в зону действия, тоже организуется подобным образом: психоэмоциональное состояние людей улучшается, вредные для человека излучения уменьшаются, исчезают геопатогенные зоны. Интернет утверждает, что если размер фигуры увеличивается в два раза, то влияние пирамиды усиливается в сто раз.

Как же всё-таки построить «Золотой» дом для себя?

Правильное распределение энергий внутри дома, гармоничные конструкции в сочетании с экологией и безопасностью строительных материалов побуждают современных архитекторов и дизайнеров использовать принципы и понятия Золотого сечения. Это увеличивает смету и создаёт впечатление глубокой проработки проекта. Стоимость возрастает на 60-80%.

Для талантливых художников и архитекторов правило сохраняется интуитивно во время творческого процесса. Однако некоторые из них сознательно реализуют это положение.

В природе подобная соразмерность встречается везде.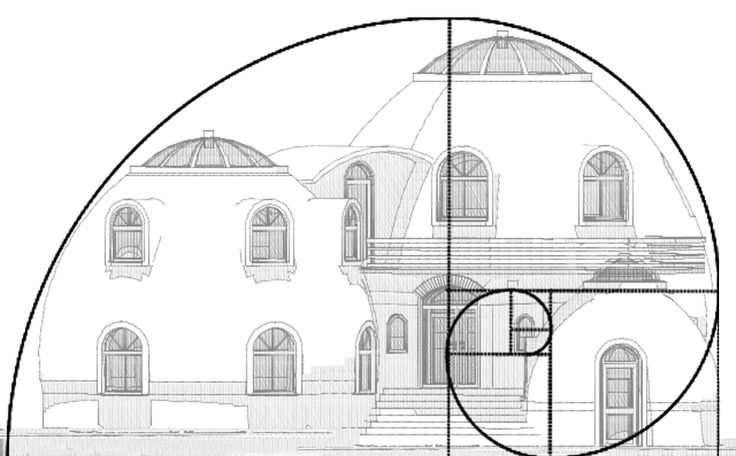 Тот, кто чувствует гармонию пространства, создаст пропорциональное здание без специальных для этого усилий.

Например, наши предки строили хоромы соразмерные человеку. Мерили высоту и длину в саженях, локтях, аршинах, пядях. Никто не возражает, что в человеческом теле соблюдена золотая пропорция? Длина руки от кончиков пальцев до подмышки относится к расстоянию от той же точки до локтя как эта величина к размеру ладони.

Известный французский архитектор Ле Корбюзье для расчёта параметров будущего дома и интерьера использовал в качестве отправной единицы рост хозяина. Все его работы по-настоящему индивидуальны и гармоничны.

5 способов соблюдать правило в интерьере

1. В доме, построенном без учёта соотношения, можно сделать перепланировку комнат, чтобы пропорции соответствовали.
2. Иногда достаточно переставить мебель или сделать дополнительную перегородку.
3. Аналогичным образом меняется высота и длина окон и дверей.
4. В цветовом оформлении получение упрощённого соотношения достигается за счёт 60% основного цвета, 30% — оттеняющего, и остальных 10% — усиливающих восприятие тонов.
5. Высота и длина мебели должна соизмеряться высотой потолков и шириной простенков.

Приложение этой нормы в интерьере, как архитектурно оформленном пространстве, объединяют с понятиями самоорганизации, рекурсии, асимметрии, красоты.

О золотом сечении простыми словами

Что же это такое? Отрезки золотой пропорции выражаются бесконечной иррациональной дробью, десятичное значение которой равно приближённо числу Ф≈1,618 или Ф≈1,62. Другими словами: если берём целое и делим его на две части так, что одна из них составляет 62%, а другая — 38%, получаем Золотую пропорцию.

Золотой прямоугольник: когда длину большей стороны делим на длину меньшей и получаем число Ф. При делении меньшей на большую получается обратное значение φ ≈ 0,618.

Золотой равнобедренный треугольник: если отношение размера одной боковой стороны и размера основания составляет золотое число Ф; угол между равными сторонами равен 36°.

Золотой прямоугольный треугольник Кеплера объединяет в себе теорему Пифагора и ЗС: соотношение квадратов его сторон составляет 1,618.

Оцените полезность статьи, поделитесь с друзьями и добавьте в закладки, чтобы было легко найти.

Смотрите познавательное видео по теме

Важность золотого сечения в архитектуре

Золотое сечение определялось с использованием различных названий как в прошлом, так и в настоящем. Фи, Золотая середина, Божественное сечение, Золотая пропорция и Божественная пропорция — вот лишь некоторые из них. почти все элементы природы состоят из этого магического соотношения (1:1,618). Золотое сечение в природе существует в форме нашей вселенной к форме человеческого тела, форме облаков к форме цветов и листьев. Это соотношение можно найти почти во всех красивых элементах природы вокруг нас.

Кредиты: Pixabay

Золотое сечение в природе существует снова и снова. Он также имеет возможность сделать элементы сбалансированными и привлекательными. Поэтому люди с древних времен использовали одну и ту же пропорцию в математике, искусстве, музыке, а также архитектуре. Попробуем лучше понять и узнать, как была выведена эта магическая пропорция.

Вывод:

Золотое сечение тесно связано с числами Фибоначчи. Вы должны быть знакомы с тем же через вашу школу или знаменитый код да Винчи.

Ниже в ряду Фибоначчи:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377……

Разделим два последовательных числа и узнать, что мы получаем.

1/1: 1, 2/1: 2, 3/2: 1,5, 5/3: 1,666, 8/5: 1,6, 13/8: 1,625, 21/13: 1,615, 34/21: 1,619, 55/34: 1,6176, 89/55: 1,6181, 144/89: 1,6179, 233/144: 1,618, 377/233: 1,618….

Соотношение последовательных чисел, кажется, устанавливается на одном уровне, т. е. 1,618. Это бесконечное явление известно как «Золотое сечение» или «Фи».

Изображение Герда Альтманна с Pixabay

Phi в основном используется для определения идеально симметричного отношения между любыми двумя элементами. Его также можно определить с помощью золотого прямоугольника. Если мы отрежем от этого прямоугольника квадрат (длина квадрата равна меньшей стороне прямоугольника), длина и ширина оставшегося прямоугольника будут иметь те же пропорции, что и исходный прямоугольник. Вы можете дальше выполнять то же упражнение с новым Золотым прямоугольником, и соотношение будет продолжаться бесконечно.

Золотое сечение в архитектуре Древние времена:

1. Египетская архитектура: Великая пирамида в Гизе (2570 г. до н.э.) – один из самых древних и лучших примеров использования фи. Отношение высоты пирамиды к любой из сторон ее основания примерно равно Фи.

Фото Спенсера Дэвиса на Unsplash

2. Древнегреческая архитектура: Почти все здания Древней Греции использовали эту пропорцию для определения отношения высоты зданий к их основанию. То же самое также использовалось для определения различных архитектурных элементов, найденных в Афинском Акрополе (468–430 гг. До н.э.). Это сделало все здания более красивыми и сбалансированными. Парфенон — один из самых известных примеров древнегреческих построек, спроектированных с использованием золотого сечения.

Фото Джоша Стюарта на Unsplash

3. Еще несколько архитектурных чудес в истории, построенных с использованием этого соотношения. Он включает в себя Великую мечеть Кайруана и ступу Боробудур на Яве, Индонезия.

4. Phi также внимательно следил за определением геометрии структур, построенных в готическом архитектурном стиле. Некоторые из самых известных сооружений включают Нотр-Дам, Пасир и Шартрский собор.

5. Он также очень часто использовался многими известными художниками в древние времена. Некоторые из самых известных произведений искусства, отражающих это соотношение, включают «Мона Лизу» и «Витрувианский человек» Винчи. Золотое сечение в искусстве также можно легко найти в различных произведениях неоимпрессионизма, кубизма, де стиля и сюрреализма.

Использование

Золотого сечения в архитектуре в последнее время:

1. Строения Ле Корбюзье: Ле Корбюзье был одним из самых важных архитекторов архитектуры модерна. Он черпал большое вдохновение из золотого сечения. Корбюзье широко использовал «Витрувианского человека» Винчи. Он также включил пропорции человеческого тела, чтобы улучшить функциональность своих архитектурных проектов.

Фото Рикардо Гомеса Анхеля на Unsplash

2. Структуры Миса ван дер Роэ: Несколько работ этого легендарного архитектора, работавшего над теорией «Меньше значит больше», изображают использование Фи. Дом Фарнсворта, как и несколько других работ Людвига Миса ван дер Роэ, черпал вдохновение в том же.

3. Ряд архитекторов, работавших в неоготическом и постмодернистском архитектурном стиле, были широко известны тем, что использовали в своих проектах эту золотую пропорцию, чтобы их конструкции выглядели сбалансированными.

Как золотое сечение может быть полезным для архитекторов?

Это волшебная пропорция, с которой должен быть знаком каждый художник и дизайнер. Они могут использовать то же самое, чтобы сделать свою работу более привлекательной и приятной для глаз. Вот некоторые из способов, которыми архитекторы могут воспользоваться:

• Для определения пропорций своих проектов: в использовании золотое сечение для определения пропорций же.
• Чтобы определить высоту любой конструкции, чтобы она выглядела более сбалансированной: Чтобы сделать структуру любого здания более привлекательной и привлекательной, архитекторы могут использовать золотое сечение. Основываясь на длине основания конструкции, можно эффективно определить видимую высоту конструкции с помощью Фи (1,618).
• Для штамповки различных интересных по дизайну форм: Очевидно, что все строения и архитектурные элементы не могут быть идеальными прямоугольниками. Архитекторы также должны использовать другие формы, чтобы сделать свой дизайн более функциональным и уникальным. К счастью, есть несколько изменений в золотом прямоугольнике, которые также могут оказаться полезными для взбивания других наших фигур с идеальными пропорциями.

Ниже перечислены некоторые из наиболее полезных изменений золотого прямоугольника:

1. Золотой треугольник: Это равнобедренный треугольник, меньшая сторона которого кратна числам Phi смежных сторон. Это может быть полезно для определения гораздо большего количества фигур, кроме треугольника.
2. Логарифмическая спираль: разделение пополам существующего золотого треугольника с другим золотым треугольником может определить форму этой спирали. В результате образуется бесконечная спиральная петля, которую можно использовать в нескольких местах при проектировании здания.

Вышеупомянутые золотые геометрические формы, в том числе золотой прямоугольник, золотой треугольник и логарифмическая спираль, могут быть очень полезны для архитекторов при определении различных сбалансированных форм для включения в проекты зданий. Однако на практике эти эмпирические правила могут быть полезны только при определении приблизительных пропорций элементов из-за ограничений, налагаемых функциональностью и используемыми материалами.

Золотое сечение было великим элементом, который веками помогал архитекторам и художникам. Это помогает им сделать их дизайн более сбалансированным и привлекательным. Вы также можете попробовать включить то же самое в любой из ваших элементов дизайна. То же самое может варьироваться от такого большого, как здание, до такого маленького, как любительское произведение искусства.

Золотое сечение в архитектуре | illustrach

Что такое золотое сечение?

Для определения золотого сечения в прошлом и в настоящем использовались разные названия. Несколько примеров включают фи, золотую середину, божественное сечение, золотую пропорцию и божественную пропорцию. Почти все элементы природы содержат это золотое сечение (1:1,618). Золотое сечение можно найти в природе во всем, от строения Вселенной до человеческого тела, от облаков до цветов и листьев. Почти все прекрасные вещи в окружающем нас мире имеют это соотношение.

В природе золотое сечение встречается неоднократно. Кроме того, он может балансировать и украшать элементы. В результате с древних времен человечество использовало одну и ту же пропорцию в математике, искусстве, музыке и строительстве. Попробуем более подробно разобраться в происхождении этой пропорции. В этой статье мы поговорим о предположениях и пионерских работах о том, как появилось золотое сечение в архитектуре.

Как золотое сечение используется в архитектуре?

Многие люди утверждают, что древние памятники имеют пропорции, близкие к 1,618, но часто полагаются на предположительные интерпретации и приблизительные измерения. Например, были сделаны утверждения относительно пропорций золотого сечения в китайских, ольмекских, египетских, шумерских и греческих вазах, а также в критских и микенских артефактах позднего бронзового века. Они появились примерно на 1000 лет раньше, чем греческие математики, которые первыми изучили золотое сечение. Однако исторические источники отрывочны, и, поскольку в анализе используются различные методологии, их сложно сравнивать. Например, говорят, что концентрические круги Стоунхенджа имеют размеры золотого сечения.

Примеры использования золотого сечения в архитектуре

Одним из старейших и лучших примеров использования числа Фи является Великая пирамида в Гизе (2570 г. до н.э.). Высота пирамиды, деленная на одну из сторон ее основания, дает отношение, примерно равное Фи.

Великая пирамида Гизы Кредит: значение золотого сечения в архитектуре – The Arch Insider

Греческие художники и архитекторы знали или применяли золотое сечение как правило пропорции для эстетики. Говорят, что строительство Акрополя началось примерно в 600 г. до н.э., хотя части, предположительно демонстрирующие пропорции золотого сечения, были изготовлены между 468 и 430 г. до н.э. У греческой богини Афины был храм под названием 9.0003 Парфенон . Говорят, что ряд золотых прямоугольников окружает фасад Парфенона, а также другие его части и другие места. Золотое сечение использовалось на западном фасаде Парфенона. Согласно различным анализам, Парфенон и Афинский Акрополь имеют множество пропорций, напоминающих золотое сечение.

Западный фасад Парфенона
Авторы и права: Список работ, созданных с использованием золотого сечения — Википедия0003 Дидимский храм Аполлона , созданный Паионием Эфесским и Дафнисом Милетским, имел золотые пропорции.

Храм Аполлона в Дидиме. Авторы и права: Храм Аполлона в Дидиме | Турецкие археологические новости (turkisharchaeonews.net)

Дизайн интерьера замка Чичен-Ица ​​ следует золотому сечению. Золотое сечение соединяет внешние области с внутренним пространством.

Замок Чичен-Ица ​​
Предоставлено: Руины Чичен-Ицы | Древние постройки, найденные в Чичен-Ице

Золотое сечение также использовалось на Великой мечети Кайруана в Тунисе. Говорят, что план, молитвенная зона, двор и минарет Великой мечети Кайруана были созданы с использованием золотого сечения.