Содержание
Зависимость мощности от силы тока, формула мощности, физический смысл
Пример HTML-страницы
Первое упоминание об электричестве встречается в опытах древнегреческого философа Фалеса. Именно он первым обнаружил, что предметы при трении притягиваются. Одноименный термин был введен в начале 17-го века английским физиком Гилбертом, после опытов, проведенных с магнитами. Отцом же науки об электричестве считается французский ученый Кулон – именно после открытия закона, получившего его имя, электротехника начала свою победную поступь, которая продолжается до сих пор. Этот закон утверждает, что два точечных заряда в безвоздушной среде взаимодействуют с силой, прямо пропорциональной их модулям и обратно – расстоянию между ними, возведенному в квадрат.
Выясним, что же представляет собой понятие электричество?
Если коротко, то это – направленное движение потока заряженных частиц. Тела, через которые они проходят, называются проводниками. Каждый проводник имеет определенное сопротивление электрическому току, которое раз
И, перед тем, как перейти к основным законам, несколько слов о заряженных частицах: они бывают, условно говоря, положительными и отрицательными. Одноименные заряды отталкиваются, а разноименные – притягиваются.
Одноименные заряды отталкиваются, а разноименные – притягиваются.
А теперь, перейдем к главному.
Основа-основ науки об электричестве – закон Ома.
Эксперимент, который провел этот немецкий физик, привел его к следующему убеждению: сила тока I, проходящего через металлический проводник, пропорциональна напряжению на его концах, или I = U/R
Здесь напряжением называется разность, образно говоря, «давлений», созданных двумя точками электрической цепи. Измеряют его в вольтах. Электрический ток представляет собой число электронов, которые пропускает участок электрической цепи и измеряется в амперах. Сопротивлением считается свойство цепи помешать этому движению. В честь упомянутого физика, его измеряют в омах. Иначе говоря, проводник, через который проходит ток в 1 ампер при напряжении в 1 вольт, обладает сопротивлением в 1 ом.
Вся остальная электротехника «пляшет» от этого.
О мощности электрического тока
В физике мощностью считают скорость выполнения работы. Неважно, какой. Чем эта операция проводится быстрее, тем большей считается мощность того, кто ее исполняет, будь то человек, механическое устройство или что-то еще.
Неважно, какой. Чем эта операция проводится быстрее, тем большей считается мощность того, кто ее исполняет, будь то человек, механическое устройство или что-то еще.
Так же и в случае с электрическим током: ее мощность представляет собой отношение работы, произведенной движущимися электрическими зарядами к промежутку времени, которое для этого понадобилось.
Проще говоря, для того, чтобы получить электрическую мощность в 1 ватт, когда источник тока имеет напряжение 1 вольт, необходимо пропустить через проводник ток в 1 ампер. Другими словами, мощность (P) можно посчитать, перемножив друг на друга электрическое напряжение и ток:
P = U*I.
Запомнив эту нехитрую формулу, на практике можно рассчитать мощность. Например, если известны значения тока и сопротивления, а о напряжении сведений нет, можем воспользоваться законом Ома, подставив в формулу вместо него I*R. Получится, что мощность равна квадрату электрического тока, помноженному на сопротивление.
Этот закон точно так же придет на помощь, если известны величины напряжения и сопротивления. В этом случае подставив вместо значения тока I = U/R, получим значение мощности, равное квадрату напряжения, поделенному на сопротивление.
Вот так – ничего сложного!
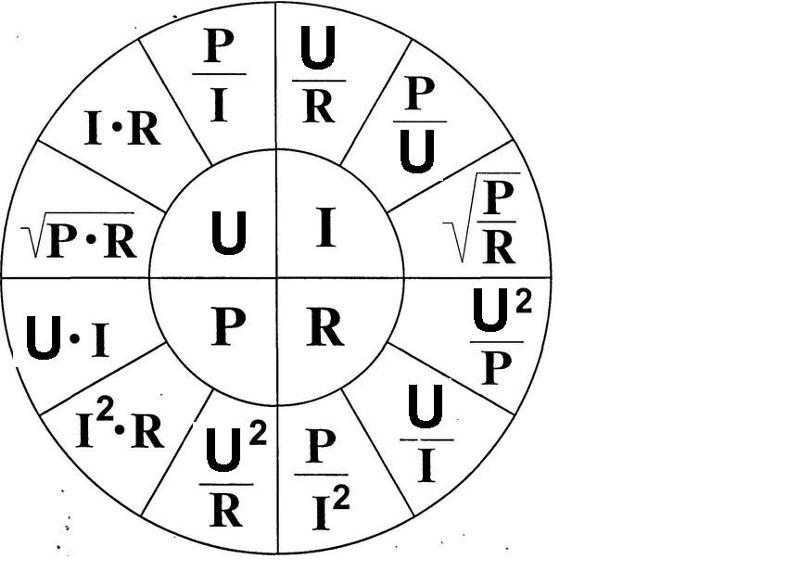
Основные электротехнические формулы. Мощность. Сопротивление. Ток. Напряжение. Закон Ома.
Основные электротехнические формулы. Мощность. Сопротивление. Ток. Напряжение. Закон Ома.
Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Физический справочник / / Электрические и магнитные величины / / Понятия и формулы для электричества и магнетизма. / / Основные электротехнические формулы. Мощность. Сопротивление. Ток. Напряжение. Закон Ома. Поделиться: |
Вы сейчас находитесь в каталоге: Основные электротехнические формулы. |
Цепь постоянного тока (или, строго говоря, цепь без комплексного сопротивления)
Применимость формул: пренебрегаем зависимостью сопротивлений от силы тока.
И еще ниже куча формулировок закона Ома для участка цепи : | |||||
НЕ ЗАБЫВАЕМ: Законы Кирхгофа они же Правила Кирхгофа для тока и напряжения.
Цепь переменного синусоидального тока c частотой ω.
Применимость формул: пренебрегаем зависимостью сопротивлений от силы тока и частоты.
Напомним, что любой сигнал, может быть с любой точностью разложен в ряд Фурье, т.е. в предположении, что параметры сети
Закон Ома для цепей переменного тока:
| |||||
19.4 Электроэнергия | Техасский шлюз
Цели обученияПрактические задачиПроверьте свое понимание
Цели обучения
К концу этого раздела вы сможете делать следующее:
- Дать определение электрической мощности и описать уравнение электрической мощности
- Расчет электрической мощности в цепях резисторов, соединенных последовательно, параллельно и комплексно
| электроэнергия |
Энергия у многих ассоциируется с электричеством. Каждый день мы используем электроэнергию для работы наших современных приборов. Линии электропередачи являются наглядными примерами электроснабжения. Мы также используем электроэнергию, чтобы заводить автомобили, компьютеры или освещать дома. Мощность — это скорость передачи энергии любого типа; электрическая мощность – это скорость, с которой электрическая энергия передается в цепи. В этом разделе мы узнаем не только, что это значит, но и какие факторы определяют электрическую мощность.
Мощность — это скорость передачи энергии любого типа; электрическая мощность – это скорость, с которой электрическая энергия передается в цепи. В этом разделе мы узнаем не только, что это значит, но и какие факторы определяют электрическую мощность.
Для начала давайте подумаем об лампочках, которые часто характеризуются номинальной мощностью в ваттах. Сравним лампочку мощностью 25 Вт с лампочкой мощностью 60 Вт (см. рис. 19.23). Хотя оба работают при одинаковом напряжении, лампа мощностью 60 Вт излучает больше света, чем лампа мощностью 25 Вт. Это говорит нам о том, что выходная мощность электрической цепи определяется не напряжением, а чем-то иным.
Лампы накаливания, такие как две, показанные на рис. 19.23, по существу представляют собой резисторы, которые нагреваются, когда через них проходит ток, и нагреваются настолько, что излучают видимый и невидимый свет. Таким образом, две лампочки на фотографии можно рассматривать как два разных резистора. В простой цепи, такой как лампочка с приложенным к ней напряжением, сопротивление определяет ток по закону Ома, поэтому мы можем видеть, что ток, как и напряжение, должен определять мощность.
Рис. 19.23 Слева — лампочка мощностью 25 Вт, справа — лампочка мощностью 60 Вт. Почему их выходная мощность различна, несмотря на то, что они работают на одном и том же напряжении?
Формулу мощности можно найти с помощью размерного анализа. Рассмотрим единицы мощности. В системе СИ мощность выражается в ваттах (Вт), что представляет собой энергию в единицу времени, или Дж/с
19,47 Вт=Джс.Вт=Джс.
Вспомним теперь, что напряжение — это потенциальная энергия на единицу заряда, а это означает, что единицы напряжения составляют Дж/Кл
19.48В=JC.V=JC.
Мы можем переписать это уравнение как J=V×CJ=V×C и подставить его в уравнение для ватт, чтобы получить
W=Js=V×Cs=V×Cs.W=Js=V×Cs=V ×Сс.
Но кулон в секунду (Кл/с) — это электрический ток, который мы можем видеть из определения электрического тока, I=ΔQΔtI=ΔQΔt, где ΔΔ Q — заряд в кулонах, а ΔΔ t — время в секундах. Таким образом, приведенное выше уравнение говорит нам, что электрическая мощность равна напряжению, умноженному на ток, или
Таким образом, приведенное выше уравнение говорит нам, что электрическая мощность равна напряжению, умноженному на ток, или
Р=IV. Р=IV.
Это уравнение дает электрическую мощность, потребляемую цепью с падением напряжения В и током I .
Например, рассмотрим схему на рис. 19.24. По закону Ома ток, протекающий через цепь, равен
19,49I=VR=12 В100 Ом=0,12 A.I=VR=12 В100 Ом=0,12 А. .50P= VI=(12 В)(0,12 А)=1,4 Вт.P=VI=(12 В)(0,12 А)=1,4 Вт.
Куда уходит эта мощность? В этой схеме мощность идет в основном на нагрев резистора в этой цепи.
Рис. 19.24 Простая схема, потребляющая электроэнергию.
При расчете мощности в цепи на рис. 19.24 мы использовали сопротивление и закон Ома для определения силы тока. Закон Ома дает ток: I=V/RI=V/R, который мы можем подставить в уравнение для электрической мощности, чтобы получить
P=IV=(VR)V=V2RP.P=IV=(VR)V= В2Р.
Мощность определяется только напряжением и сопротивлением.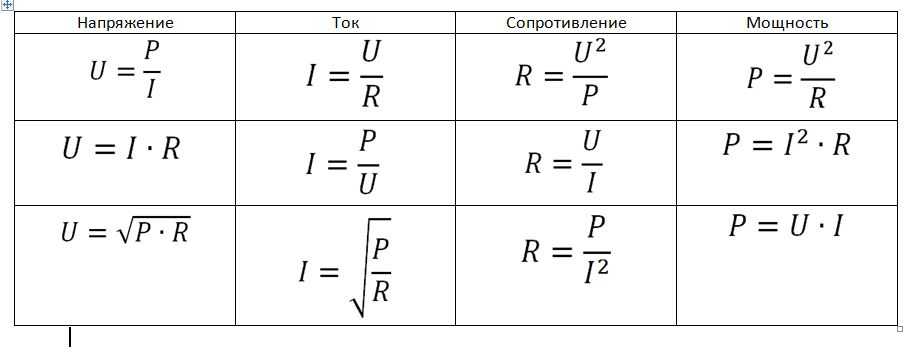
Мы также можем использовать закон Ома, чтобы исключить напряжение из уравнения для электрической мощности и получить выражение для мощности только через ток и сопротивление. Если мы запишем закон Ома как V=IRV=IR
и используйте это, чтобы устранить V в уравнении P=IVP=IV получаем
P=IV=I(IR)=I2R.P=IV=I(IR)=I2R.
Мощность определяется только током и сопротивлением.
Таким образом, комбинируя закон Ома с уравнением P=IVP=IV для электрической мощности, мы получаем еще два выражения для мощности: одно через напряжение и сопротивление, а другое через ток и сопротивление. Обратите внимание, что в выражения для электрической мощности входят только сопротивление (а не емкость или что-то еще), ток и напряжение. Это означает, что физической характеристикой цепи, которая определяет, сколько мощности она рассеивает, является ее сопротивление. Любые конденсаторы в цепи не рассеивают электроэнергию — наоборот, конденсаторы либо хранят электроэнергию, либо отдают ее обратно в цепь.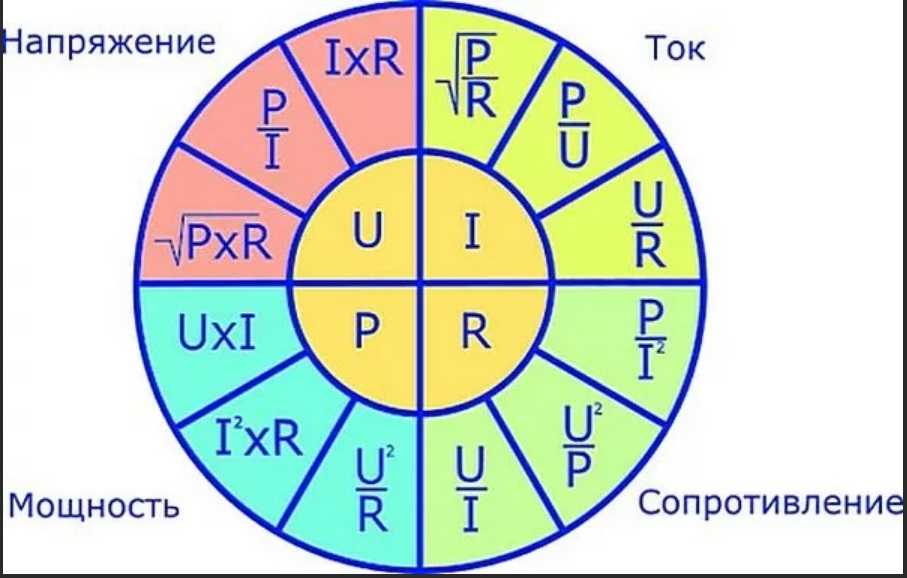
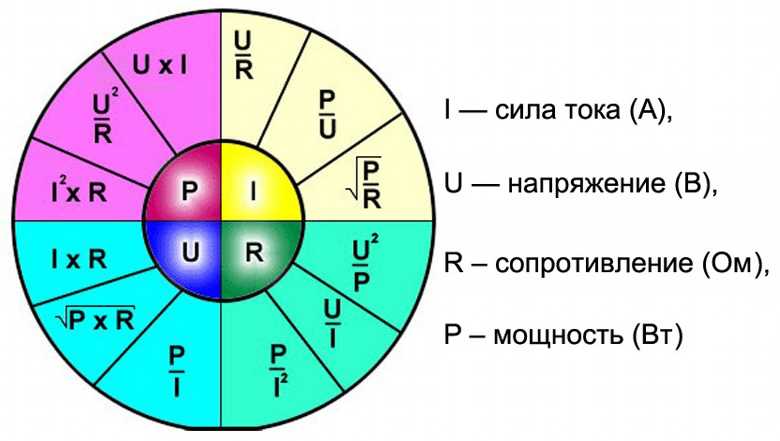
Чтобы понять, как связаны между собой напряжение, сопротивление, ток и мощность, рассмотрите рис. 19.25, на котором показано колесо формул . Величины в центральной четверти окружности равны количествам в соответствующей внешней четверти окружности. Например, чтобы выразить потенциал V через мощность и ток, мы видим из круга формул, что V=P/IV=P/I.
Рис. 19.25 Колесо формул показывает, как соотносятся вольты, сопротивление, ток и мощность. Количества во внутренних четвертях кругов равны количествам в соответствующих внешних четвертях кругов.
Рабочий пример
Найти сопротивление лампочки
Типичная старая лампочка накаливания имела мощность 60 Вт. Если предположить, что на лампочку подается напряжение 120 В, какова сила тока через лампочку?
СТРАТЕГИЯ
Нам известны напряжение и выходная мощность простой цепи, содержащей лампочку, поэтому мы можем использовать уравнение P=IVP=IV, чтобы найти ток I , протекающий через лампочку.
Решение
Решение P=IVP=IV для тока и подстановка заданных значений напряжения и мощности дает
19.51P=IVI=PV=60 W120 V=0,50 A.P=IVI=PV=60 W120 V=0,50 A.
Таким образом, через лампочку проходит полампера, когда на нее подается напряжение 120 В.
Обсуждение
Это значительный ток. Напомним, что бытовая электроэнергия является переменным, а не постоянным током, поэтому 120 В, подаваемые из бытовых розеток, представляют собой переменную, а не постоянную мощность. 120 В — это фактически усредненная по времени мощность, выдаваемая такими розетками. Таким образом, средний ток, проходящий через лампочку за период времени, превышающий несколько секунд, составляет 0,50 А.
Пример работы
Грелки для ботинок
Чтобы согреть ботинки в холодные дни, вы решили вшить в стельку ботинок схему с несколькими резисторами. Вам нужно 10 Вт тепла от резисторов в каждой стельке, и вы хотите питать их от двух 9-вольтовых батарей (соединенных последовательно). Какое общее сопротивление вы должны оказывать на каждую стельку?
Какое общее сопротивление вы должны оказывать на каждую стельку?
СТРАТЕГИЯ
Мы знаем желаемую мощность и напряжение (18 В, потому что у нас есть две 9-вольтовые батареи, соединенные последовательно), поэтому мы можем использовать уравнение P=V2/RP=V2/R, чтобы найти необходимое сопротивление .
Решение
Решая P=V2/RP=V2/R для сопротивления и подставляя данные напряжения и мощности, мы получаем
19,52P=V2RR=V2P=(18 V)210 W=32 Ω.P=V2RR =V2P=(18 В)210 Вт=32 Ом.
Таким образом, общее сопротивление в каждой стельке должно быть 32 Ом.Ом.
Обсуждение
Давайте посмотрим, какой ток будет проходить по этой цепи. К сопротивлению 32 Ом приложено напряжение 18 В, поэтому закон Ома дает0003
Все аккумуляторы имеют этикетки, на которых указано, сколько заряда они могут обеспечить (в пересчете на ток, умноженный на время). Типичная щелочная батарея 9 В может обеспечить заряд 565 мА⋅чмА⋅ч.
(таким образом, две батареи 9 В обеспечивают 1130 мА⋅чмА⋅ч), поэтому эта система отопления будет работать в течение времени
19,54t=1130×10−3 A⋅ч0,56 A=2,0 ч. t=1130×10−3 А⋅ч0,56 А=2,0 ч.
t=1130×10−3 А⋅ч0,56 А=2,0 ч.
Рабочий пример
Мощность через ветвь цепи
Сопротивление каждого резистора в схеме ниже составляет 30 Ом. Какая мощность рассеивается на средней ветви цепи?
СТРАТЕГИЯ
Средняя ветвь схемы содержит последовательно соединенные резисторы R3 и R5R3 и R5. Напряжение на этой ветви составляет 12 В. Сначала мы найдем эквивалентное сопротивление в этой ветви, а затем с помощью P=V2/RP=V2/R найдем мощность, рассеиваемую в ветви.
Решение
Эквивалентное сопротивление равно Rmiddle=R3+R5=30 Ω+30 Ω=60 ΩRmiddle=R3+R5=30 Ω+30 Ω=60 Ω. Мощность, рассеиваемая средней ветвью цепи, составляет
19,55Pmiddle=V2Rmiddle=(12 В)260 Ом=2,4 Вт.Pmiddle=V2Rmiddle=(12 В)260 Ом=2,4 Вт.
Обсуждение
Давайте посмотрим, сохраняется ли энергия в этой цепи, сравнив мощность, рассеиваемую в цепи, с мощностью, выдаваемой батареей. Во-первых, эквивалентное сопротивление левой ветви равно
19,56Rleft=11/R1+1/R2+R4=11/30 Ом+1/30 Ом+30 Ом=45 Ом. Rleft=11/R1+1/R2 +R4=11/30 Ом+1/30 Ом+30 Ом=45 Ом.
Rleft=11/R1+1/R2 +R4=11/30 Ом+1/30 Ом+30 Ом=45 Ом.
Мощность через левую ветвь
19,57Pleft=V2Rleft=(12 В)245 Ом=3,2Вт.Pleft=V2Rleft=(12 В)245 Ом=3,2 Вт.
Правая ветвь содержит только R6R6 , так эквивалентное сопротивление равно Rright=R6=30 ΩRright=R6=30 Ω. Мощность через правую ветвь равна
19,58Pright=V2Rright=(12 В)230 Ом=4,8Вт.Pright=V2Rright=(12 В)230 Ом=4,8 Вт
Полная мощность, рассеиваемая цепью, представляет собой сумму мощностей, рассеиваемых в каждой ветви .
19.59P=Pleft+Pmiddle+Pright=2,4 W+3,2 W+4,8 W=10,4 WP=Pleft+Pmiddle+Pright=2,4 W+3,2 W+4,8 W=10,4 Вт
Мощность, обеспечиваемая батарея
19.60P=IV.P=IV.
, где I — общий ток, протекающий через батарею. Поэтому мы должны сложить токи, проходящие через каждую ветвь, чтобы получить я . Ответвления вносят токи
19.61Ileft=VRleft=12 V45 Ω=0.2667 AImiddle=VRmiddle=12 V60 Ω=0.20 AIright=VRright=12 V30 Ω=0. 40 A.Ileft=VRleft=12 V4 5 Ω=0,2667 AImiddle=VRmiddle= 12 V60 Ω=0,20 AIright=VRright=12 V30 Ω=0,40 A. A=0,87 A.I=Iлевый+средний+Iправый =0,2667 A+0,20 A+0,40 A=0,87 A.
40 A.Ileft=VRleft=12 V4 5 Ω=0,2667 AImiddle=VRmiddle= 12 V60 Ω=0,20 AIright=VRright=12 V30 Ω=0,40 A. A=0,87 A.I=Iлевый+средний+Iправый =0,2667 A+0,20 A+0,40 A=0,87 A.
и мощность, обеспечиваемая аккумулятором, равна
19,63P=IV=(0,87 A)(12 В)=10,4 W.P=IV=(0,87 A )(12 В)=10,4 Вт.
Это та же мощность, которая рассеивается на резисторах цепи, что показывает сохранение энергии в этой цепи.
Практические задания
Какова формула мощности, рассеиваемой на резисторе?
- Формула мощности, рассеиваемой на резисторе: P=IV.P=IV.
- Формула для мощности, рассеиваемой на резисторе: P=VI.P=VI.
- Формула для мощности, рассеиваемой на резисторе: P = IV .
- Формула для мощности, рассеиваемой на резисторе: P = I 2 В .
Какова формула для мощности, рассеиваемой резистором, при заданном его сопротивлении и напряжении на нем?
- Формула мощности, рассеиваемой на резисторе: P=RV2P=RV2
- Формула мощности, рассеиваемой на резисторе: P=V2RP=V2R
- Формула мощности, рассеиваемой на резисторе: P=V2RP=V2R
- Формула для мощности, рассеиваемой на резисторе: P=I2RP=I2R
Проверьте свое понимание
Упражнение 8
Какие элементы схемы рассеивают мощность?
- конденсаторы
- катушки индуктивности
- идеальные переключатели
- резисторы
Упражнение 9
Объясните словами уравнение для мощности, рассеиваемой на данном сопротивлении.
- Электрическая мощность пропорциональна току через резистор, умноженному на квадрат напряжения на резисторе.
- Электрическая мощность пропорциональна квадрату тока через резистор, умноженному на напряжение на резисторе.
- Электрическая мощность пропорциональна току через резистор, деленному на напряжение на резисторе.
- Электрическая мощность пропорциональна току через резистор, умноженному на напряжение на резисторе.
- Печать
- Поделиться
Калькулятор мощности, напряжения, тока и сопротивления
Этот калькулятор основан на простом законе Ома. Как мы уже поделились Калькулятор закона Ома (P, I, V, R) В котором вы также можете рассчитать трехфазный ток.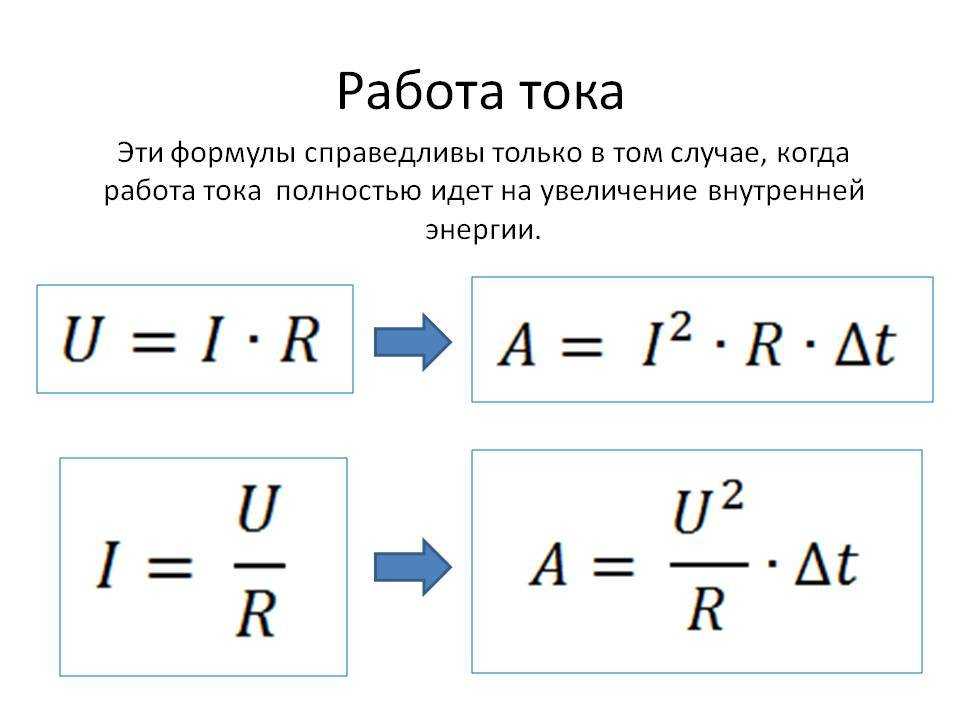 Но мы разработали его специально для цепей постоянного тока (а также для работы с однофазными цепями переменного тока без коэффициента мощности… (Мы поделимся другим калькулятором для расчета коэффициента мощности).
Но мы разработали его специально для цепей постоянного тока (а также для работы с однофазными цепями переменного тока без коэффициента мощности… (Мы поделимся другим калькулятором для расчета коэффициента мощности).
- Связанная запись: Калькулятор цветового кода резистора — расчет 3-, 4-, 5- и 6-полосных резисторов
Калькулятор мощности, напряжения, тока и сопротивления
Введите любые два из следующих значений и нажмите кнопку расчета. В результате отобразятся рассчитанные значения.
| Мощность (Вт): | ||
| Напряжение (В): | ||
| Ток (А): | ||
| Сопротивление (Ом): | ||
Формулы мощности, напряжения, тока и сопротивления
Ниже приведены возможные формулы и уравнения для этого калькулятора
(1) Формулы электрической мощности в цепях постоянного тока
(2) Формула электрического потенциала или напряжения в цепях постоянного тока
- В = I x R
- В = П/Я
- В = √ (П x Р)
(3) Формулы электрического тока в цепи постоянного тока
- I=V/R
- I = P/V
- I = √P/R
(4) Формулы электрического сопротивления
- R = V/I
- R = P/I 2
- Р = В 2 /P
*Где
- I = ток в амперах (А)
- В = напряжение в вольтах (В)
- P = мощность в ваттах (Вт)
- R = сопротивление в Ом (Ом)
Связанные электрические калькуляторы:
- Калькулятор мощности, напряжения, тока и сопротивления (P, V, I, R)
- Калькулятор автоматического выключателя Калькулятор с примерами
- Усовершенствованный калькулятор падения напряжения
- Калькулятор размеров электрических проводов и кабелей (медь и алюминий)
- AWG/SWG в мм/мм2, дюйм/дюйм3 и тыс.

 Мощность. Сопротивление. Ток. Напряжение. Закон Ома.
Мощность. Сопротивление. Ток. Напряжение. Закон Ома.