Содержание
Калькулятор кубов бруса — сколько штук в кубе + таблица
Содержание
- 1 Сколько штук бруса в кубе: онлайн калькулятор
- 2 Брус длинною 6 метров: сколько штук в кубе. Таблица с расчетами
- 3 Количество бруса в кубе — как рассчитать количество бруса?
- 3.1 Как перевести погонные метры в кубические?
Сколько штук бруса в кубе: онлайн калькулятор
калькулятор количества бруса в кубе
В строительстве любого каркасного дома требуется закупка бруса, так как этот материал используется при сборке венцов сруба и возведении крыши. Кроме того, брус применяется в изготовлении многих других деревянных конструкций. Чтобы избежать ошибок, важно научиться определять количество бруса в кубометре.
Данная операция отличается очень простой математической схемой. Объем любого предмета прямоугольной формы вычисляется путем умножения его ширины и высоты на длину. При покупке большого количества бруса, имеющего разную длину и сечение, могут возникать различные сложности. В результате сумма переплаты может оказаться достаточно большой.
В результате сумма переплаты может оказаться достаточно большой.
Эта статься посвящена нюансам подсчета количества бруса в одном кубе. Мы предлагаем познакомиться с калькулятором и удобными в использовании таблицами «шпаргалками». Это поможет легко перевести погонные метры бруса в кубы.
Брус длинною 6 метров: сколько штук в кубе. Таблица с расчетами
Таблица — количества 6 метрового бруса в кубе
Количество бруса в кубе — как рассчитать количество бруса?
Для расчета кубатуры на дом и определения точного количества брусьев необходимо произвести простые расчеты. Для этого нужные некоторые сведения: объем пиломатериалов и объем штучного изделия. Это необходимо для деления одной величины на другую. В приведенной ниже таблице представлены самые распространенные размеры сечений. При этом длина материала составляет 6 метров.
Формула расчета количества штук бруса в кубе 150 * 150 * 6000:
0,15 (м) * 0,15 (м) * 6 (м) = 0,135 куб.м
1 м³ / 0,135 м³ = 7 штук в кубе.
Как перевести погонные метры в кубические?
Расчет количества бруса в одном кубе продаваемого материала может рассчитать даже обычный школьник. В качестве примера для расчета количества бруса размером 150*150 в одном кубе древесины необходимо произвести следующие действия. Размер грани балки бруса, который указывается в миллиметрах, возводится в квадрат. Затем 100000 нужно разделить на то значение, которое получилось. В результате выясняется, что в одном кубе содержится 44,4 погонных метров материала. Количество шестиметровых балок в кубе будет равно 7,4 штук. Четырехметровых балок в нем будет 11 штук.
Производители и продавцы пиломатериалов не всегда бывают честными по отношению к покупателям. Сечение бруса нередко занижается по сравнению с заявленным. Часто получается, что продаваемый брус размером 150 × 200 по факту имеет сечение 140 × 190. Прежде, чем покупать брус, нужно проверить реальные параметры материала. Также важно узнать у продавца о формировании цены за куб материала.
Также важно узнать у продавца о формировании цены за куб материала.
- 5
- 4
- 3
- 2
- 1
(22 голоса, в среднем: 3.3 из 5)
Как посчитать кубатуру бруса? |
Постройка дома или бани из бруса требует основательной подготовки. Нужно разработать проект, изучить особенности обработки и утепления здания из бруса, правильно рассчитать количество необходимого материала — то есть кубатуру бруса. Как это сделать правильно?
Кубатура бруса – это значение, которое показывает: сколько бруса в кубическом метре (каким количеством бруса можно заполнить определенный объем)
Кубатура — это универсальная единица измерения бруса, используемая в строительстве. В кубах его продают и покупают. Это намного удобнее, чем в штуках.
Расчет кубатуры бруса необходим для решения нескольких проблем:
— без понимания — сколько нужно бруса для постройки того или иного здания — вы не сможете его купить. В подавляющем большинстве случаев брус продается не в штуках, а в кубометрах.
В подавляющем большинстве случаев брус продается не в штуках, а в кубометрах.
— кубатура бруса необходима для составления сметы стройки. Зная, сколько кубов бруса вам нужно (и сколько стоит один куб), вы легко посчитаете какая сумма необходима на его закупку;
— выбор средства транспортировки. Заказывая транспорт для перемещения бруса с одного места на другое вам необходимо знать, какой объем бруса вы будете перевозить;
— точно зная сколько кубов бруса необходимо для вашего дома, вы убережете свой кошелек от растрат на лишний брус, а себя — от необходимости в срочном порядке докупать недостающее.
Как посчитать кубатуру бруса?
Как показывает практика не все знают, как правильно рассчитывается кубатура бруса.
Существует несколько популярных способов, с помощью которых вы легко сможете перевести брус в кубометры:
— расчет по формуле. Несложные математические подсчеты помогут определить сколько штук бруса в одном кубе, и сколько кубов в одной штуке бруса.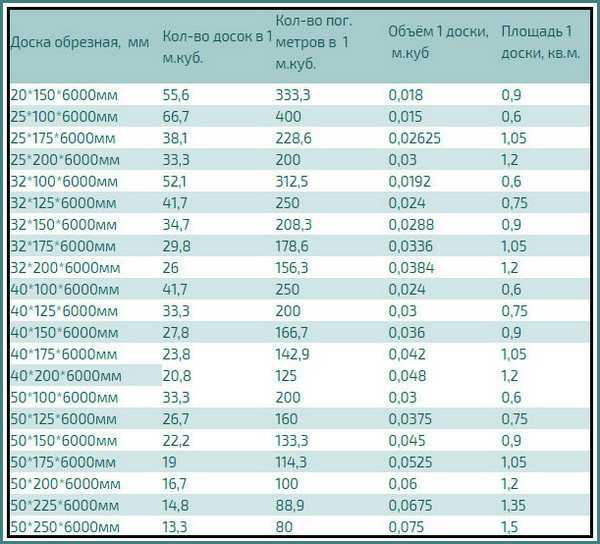
Для этого необходимо знать параметры самого бруса, его сечение. Они бывают разными: 150Х150, 100Х150, 100Х100, 150Х200, 200Х200, 100Х200 миллиметров. Для жилых домов чаше всего используют брус сечением 150Х150 миллиметров. Также необходимо знать длину бруса (чаще всего 6 метров).
Чтобы узнать объем одного бруса необходимо его ширину умножить на толщину и на длину. Например, для бруса сечением 150Х150 мм объем будет рассчитан так :0,15 мх0,15мх6м=0,135 метров кубических в одном брусе.
Если вам нужно знать, сколько штук бруса в одном кубе, то необходимо 1 метр кубический разделить на объем одного бруса. Например, 1/0, 135=74 штуки бруса в одном кубическом метре.
Соответственно, если вы знаете сколько штук бруса необходимо для строительства дома, то вы умножаете ширину на толщину, на длину и на количество бруса и получаете значение сколько кубов бруса нужно на дом. Кубатура бруса необходимая для постройки дома так же легко рассчитывается таким способом длину стен здания необходимо умножить на его высоту и на толщину бруса;
— второй современный и очень простой способ расчета кубатуры бруса – это онлайн калькулятор.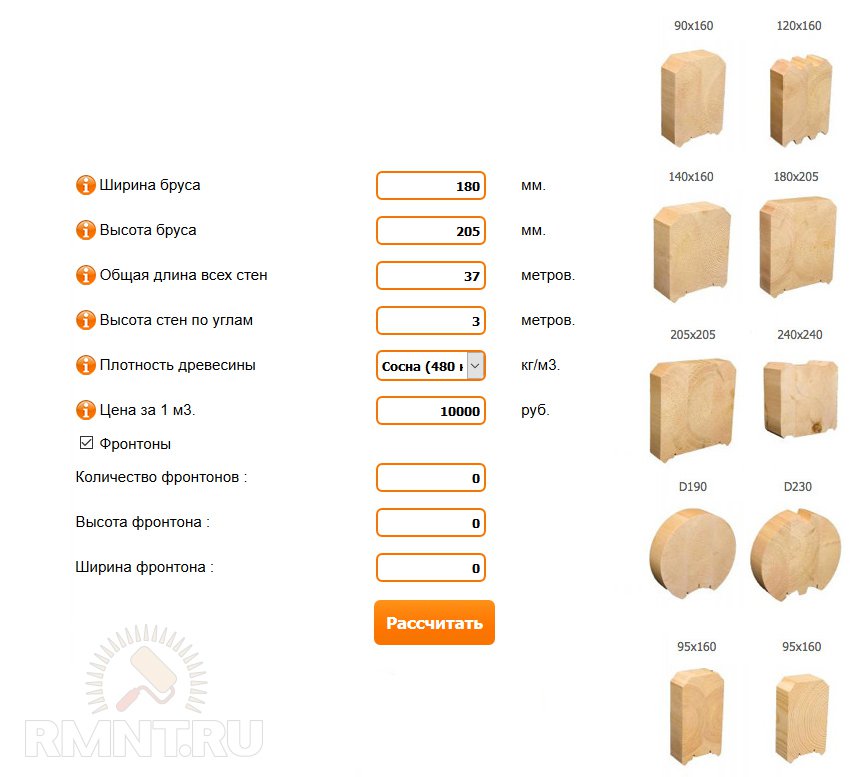 Такие калькуляторы легко и точно посчитают какая кубатура бруса. Все, что вам необходимо это ввести туда параметры бруса и нажать кнопку, через несколько секунд у вас будет готовое значение. Но есть один минус – калькулятор не поможет вам если нет доступа в интернет;
Такие калькуляторы легко и точно посчитают какая кубатура бруса. Все, что вам необходимо это ввести туда параметры бруса и нажать кнопку, через несколько секунд у вас будет готовое значение. Но есть один минус – калькулятор не поможет вам если нет доступа в интернет;
— еще один простой и доступный метод с помощью, которого легко узнать кубатуру бруса – это таблицы. Сколько бруса в кубе таблица легко вам покажет. В таких таблицах сведены уже просчитанные значения сколько бруса разного сечения в одном кубометре и сколько штук бруса определенного сечения в одном кубометре. Такую таблицу можно распечатать и всегда иметь с собой при необходимости.
Кубатура бруса таблица.
Размер Объем 1-й штуки Штук в 1 м³
100×100×6000 мм 0,06 м³ 16 шт.
100×150×6000 мм 0,09 м³ 11 шт.
150×150×6000 мм 0,135 м³ 7 шт.
100×180×6000 мм 0,108 м³ 9 шт.
150×180×6000 мм 0,162 м³ 6 шт.
180×180×6000 мм 0,1944 м³ 5 шт.
100×200×6000 мм 0,12 м³ 8 шт.
150×200×6000 мм 0,18 м³ 5,5 шт.
180×200×6000 мм 0,216 м³ 4,5 шт.
200×200×6000 мм 0,24 м³ 4 шт.
250×200×6000 мм 0,3 м³ 3 шт.
Ирина Железняк, Собкор интернет-издания «AtmWood. Дерево-промышленный вестник»
Калькулятор нагрузки на балку
Калькулятор нагрузки на балку поможет вам определить реакции на опоры свободно опертой балки, вызванные вертикальными точечными нагрузками или силами. В этом калькуляторе мы рассмотрим следующее:
- Что такое реакция поддержки;
- Как рассчитать опорные реакции в балке;
- Пример расчета по нахождению опорных реакций; и
- Как рассчитать допустимую нагрузку на балку с помощью этого калькулятора нагрузки на балку.

Знание того, как найти опорные реакции, является отличным началом при анализе балок, например, при определении прогиба балки. Продолжайте читать, чтобы узнать больше.
🙋 Если вам интересно, как рассчитать прогиб балки, у нас есть наш калькулятор прогиба балки, который вы можете проверить, или наш многофункциональный калькулятор пролета деревянной балки для углубленного расчета конструкции деревянной балки.
Что такое реакция поддержки?
Согласно третьему закону движения Ньютона , каждая сила, действующая на объект, имеет равную и противоположную реакцию. Если вы пытаетесь на что-то надавить, скажем, на стену, вам кажется, что стена тоже отталкивает вас. Именно это явление описывает третий закон движения Ньютона.
В машиностроении элементы конструкции, такие как балки и колонны, взаимодействуют друг с другом в точках, где они встречаются. Представьте себе балку, которая поддерживается двумя колоннами. Вес балки давит на колонны, и из-за третьего закона движения Ньютона мы также можем сказать, что колонны воздействуют на балку эквивалентной противоположной реактивной силой. Мы называем эти силы реакции реакции поддержки .
Вес балки давит на колонны, и из-за третьего закона движения Ньютона мы также можем сказать, что колонны воздействуют на балку эквивалентной противоположной реактивной силой. Мы называем эти силы реакции реакции поддержки .
Вы можете представить дверной потолок в виде балки, показанной выше, и две домкратные стойки (вертикальные стойки, на которые опирается дверной потолок) в качестве двух опорных конструкций дверного профиля. Узнайте больше о размерах дверных перемычек, воспользовавшись нашим калькулятором размеров дверных перемычек.
На свободно опертой балке опорные реакции на каждом конце балки могут быть либо равны друг другу, либо иметь разные значения. Их значения зависят от приложенных к балке нагрузок. Если на более близком расстоянии от одной опоры находится больше нагрузок, эта опорная конструкция испытывает большую силу и, следовательно, испытывает большую реакцию.
Как рассчитать опорные реакции в балке?
Поскольку опорные реакции действуют в направлении, противоположном силе, можно сказать, что вся система находится в равновесии. Это означает, что балка не движется, а сумма сил и моментов дает ноль. Приравняв момента от нагрузки к моментам от опорных реакций , мы можем определить реакции на опорах.
Это означает, что балка не движется, а сумма сил и моментов дает ноль. Приравняв момента от нагрузки к моментам от опорных реакций , мы можем определить реакции на опорах.
Как и при расчете крутящего момента, мы также можем выполнить суммирование моментов на каждой опоре для расчета реакций. Ниже мы выражаем сумму ∑\small \sum∑ моментов на опоре A, чтобы найти реакцию на опоре B, обозначенную как RB\small R_\text{B}RB, как показано ниже: 9n(F_i\times x_i) — (R_\text{B}\times\text{span}) = 0
i=1∑n(Fi×xi)−(RB×span)=0
или
(F1×x1) + (F2×x2) + (F3×x3) + … + (Fn×xn) − (RB×span)=0,\small
(F_1\x_1 раз)\! +\! (F_2\x_2 раз)\! +\! (F_3\x_3 раз)\! +\\
…\! +\!(F_n\times x_n)\! -\! (R_\text{B}\times \text{span}) = 0,(F1×x1)+(F2×x2)+(F3×x3)+…+(Fn× xn)−(RB×span)=0,
, где:
- F1F_1F1, F2F_2F2, F3F_3F3 и FnF_nFn — точечные нагрузки на балку на расстояниях x1x_1x1, x2x_2x2, x3x_3x3, и xnx_nxn от опоры A соответственно;
- RBR_\text{B}RB – Реакция на поддержке B; и
- span\text{span}span – Длина балки между опорой A и опорой B.

Преобразовав уравнение, мы можем изолировать RBR_\text{B}RB следующим образом:
RB × span= (F1×x1) + (F2×x2)+ (F3×x3)+. .. + (Fn×xn)\маленький
\начать{выравнивать*}
Р_\текст{В}\! \раз\! \text{span} =\ & (F_1\times x_1)\! +\! (F_2\умножить на x_2)\\ &+\ (F_3\умножить на x_3)\\
& +…\! +\!(F_n\times x_n)\\
\end{align*}RB×span= (F1×x1)+(F2×x2)+ (F3×x3)+…+(Fn×xn)
RB= [(F1×x1) + (F2×x2) +(F3×x3)+…+(Fn×xn)]/span ✔\small
\начать{выравнивать*}
R_\text{B} =\ &[(F_1\times x_1)\! +\! (F_2\умножить на x_2)\!\\ &+ (F_3\умножить на x_3)\\
& +… +(F_n\times x_n)] / \text{span}\ \text{✔}
\end{align*}RB= [(F1×x1)+(F2×x2)+(F3×x3)+…+(Fn×xn)]/span ✔
Теперь, когда у нас есть выражение для нахождения RB\small R_\text{B}RB, и поскольку мы знаем, что общие приложенные силы равны сумме реакций, теперь мы можем также найти реакцию на опоре A , RA\small R_\text{A}RA, используя следующие уравнения: 9n F_i — R_\text{B}\ \text{✔}RA=i=1∑nFi−RB ✔
Теперь, когда мы знаем, как рассчитать опорные реакции в балках, давайте теперь рассмотрим пример расчет, чтобы укрепить наши знания об этом. 🙂
🙂
Пример расчета по нахождению опорных реакций
Предположим, что у нас есть 4,0-метровая свободно опертая балка с приложенной точечной нагрузкой 10,0 килоньютонов (кН) в 2,0 метрах от опоры A и другой приложенной 3,5 кН точечная нагрузка 1,5 метра от опоры B , как показано ниже:
Для расчета RB\small R_\text{B}RB сформулируем уравнение моментного равновесия следующим образом:
RB=(F1×x1)+(F2×x2)span= (10 кН×2,0 м)+(3,5 кН×(4,0 м−1,5 м))4,0 м=20 кН-м+8,75 кН-м4,0 м=7,1875 кН\scriptsize
\начать{выравнивать*}
&R_\text{B} = \frac{(F_1\times x_1)\! +\! (F_2\times x_2)}{\text{span}}\\[1.2em]
&= \frac{(10\ \text{kN}\!\times\! 2.0\ \text{m})\! +\! (3,5\ \text{кН}\!\times\! (4,0\ \text{м}\! -\! 1,5\ \text{м}))}{4,0\ \text{м}}\\[1,2 Эм]
&= \frac{20\ \text{кН-м} + 8,75\ \text{кН-м}}{4,0\ \text{м}}\\[1,2см]
&= 7,1875\ \text{кН}
\end{align*}RB=span(F1×x1)+(F2×x2)=4,0 м(10 кН×2,0 м)+(3,5 кН×(4,0 м−1,5 м)) =4,0 м20 кН-м+8,75 кН-м=7,1875 кН
Выполняя суммирование сил, получаем:
∑F=0F1+F2+(−RA)+(−RB)=010+3,5+(−RA)+(−7,1875)=0RA=10+3,5 −7,1875RA=6,3125 кН\!\размер сценария
\начать{выравнивать*}
\сумма F\! &= 0\\
Ф_1\! +\! Ф_2\! +\! (-R_\текст{А})\! +\! (-R_\текст{B})\! &= 0\\
10\! +\! 3,5\! +\! (-R_\текст{А})\! +\! (-7. 1875)\! &= 0\\
1875)\! &= 0\\
Р_\текст{А}\! &= 10\! +\! 3,5\! -7.1875\\
Р_\текст{А}\! &= 6,3125\ \text{кН}
\end{align*}∑FF1+F2+(-RA)+(-RB)10+3.5+(-RA)+(-7.1875)RARA=0=0=0= 10+3,5−7,1875=6,3125 кН
Обратите внимание , что для этого суммирования , мы рассмотрели все нисходящие силы как положительные и все направленные вверх силы как отрицательные . Основываясь на наших расчетах, приведенных выше, мы получили, что реакции на опорах A и B равны 6,3125 кН и 7,1875 кН соответственно.
Также обратите внимание, что в этом примере расчета опорных реакций и в калькуляторе нагрузки на балку мы предполагали, что балка невесома. Однако, если указан вес балки, вы можете рассматривать вес балки как еще одну направленную вниз нагрузку в центре или центроиде балки.
Использование нашего калькулятора нагрузки на балку
Наш калькулятор прост и удобен в использовании. Все, что вам нужно сделать, это ввести пролет балки , величину точечных нагрузок и их расстояния от опоры A .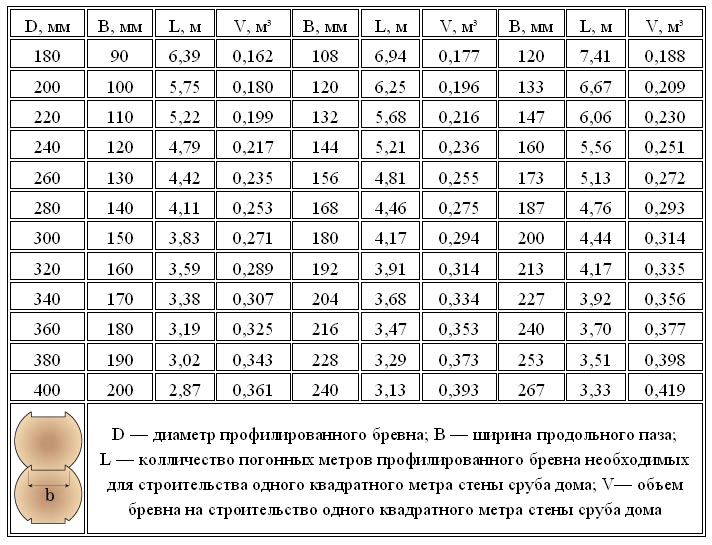 Сначала вы увидите только поля для двух загрузок (Загрузка 1 и Загрузка 2), но как только вы введете значение для x2\small x_2x2, появятся поля для Загрузки 3 и так далее.
Сначала вы увидите только поля для двух загрузок (Загрузка 1 и Загрузка 2), но как только вы введете значение для x2\small x_2x2, появятся поля для Загрузки 3 и так далее.
Если вы хотите ввести восходящую нагрузку, просто введите отрицательное значение для величины нагрузки. Всего в наш калькулятор нагрузки на балку можно ввести до 11 точечных нагрузок.
Расчет нагрузок на перемычки и балки — Строительные технологии
Обратите внимание: Эта старая статья нашего бывшего преподавателя остается доступной на нашем сайте для архивных целей. Некоторая информация, содержащаяся в нем, может быть устаревшей.
Понимание того, как нагрузки передаются через конструкцию и действуют на элементы конструкции, является первым шагом к определению размеров коллекторов и балок.0002 Большинство строителей автоматически выбирают двойные перемычки -2 x 8 или -2 x 10 для обрамления окон и дверей в каждом доме, который они строят. Эти заголовки работают, чтобы выдерживать большинство жилых нагрузок и, по совпадению, удерживают верхние части окон на одинаковой высоте. Изящное решение, но является ли это эффективным и экономичным использованием материала? То же самое относится и к балкам, таким как коньковые балки и центральные балки. Слишком часто строители собирают 2-дюймовые пиломатериалы для поддержки нагрузки на крышу и пол, не рассматривая другие варианты. Вы не можете превзойти пиломатериалы для большинства небольших оконных переплетов, но по мере увеличения пролетов и нагрузок более прочные материалы являются лучшим выбором. Пиломатериалы ограничивают возможности дизайна, а в некоторых случаях просто не работают. Parallam, Timberstrand, Laminated Veneer Lumber и Anthony Power Beam являются примерами альтернативных материалов, которые предоставляют строителям интересный выбор.
Изящное решение, но является ли это эффективным и экономичным использованием материала? То же самое относится и к балкам, таким как коньковые балки и центральные балки. Слишком часто строители собирают 2-дюймовые пиломатериалы для поддержки нагрузки на крышу и пол, не рассматривая другие варианты. Вы не можете превзойти пиломатериалы для большинства небольших оконных переплетов, но по мере увеличения пролетов и нагрузок более прочные материалы являются лучшим выбором. Пиломатериалы ограничивают возможности дизайна, а в некоторых случаях просто не работают. Parallam, Timberstrand, Laminated Veneer Lumber и Anthony Power Beam являются примерами альтернативных материалов, которые предоставляют строителям интересный выбор.
В этой серии статей, состоящей из двух частей, мы рассмотрим, как пиломатериалы и эти конструкционные материалы используются в качестве перемычек и балок. Часть I покажет вам, как проследить структурные нагрузки на коллекторы и балки. В части II будут рассмотрены процедуры определения размеров, характеристики и стоимость этих материалов для нескольких применений (см.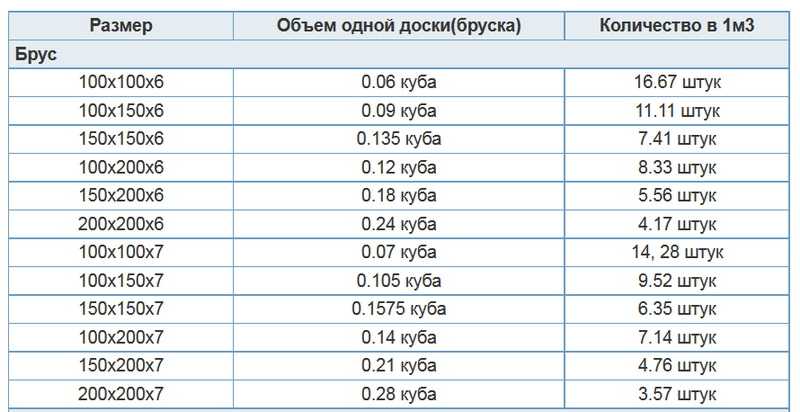 «Определение размеров спроектированных балок и коллекторов» для части 2).
«Определение размеров спроектированных балок и коллекторов» для части 2).
Выполнение работы
Работа коллекторов и балок проста. Они передают нагрузки сверху на фундамент снизу через сеть конструктивных элементов. Идея определения размеров коллекторов и балок проста: сложите вместе все временные и постоянные нагрузки, действующие на стержень, а затем выберите материал, который выдержит эту нагрузку. Балка должна быть достаточно прочной, чтобы не сломаться (значение Fb), и достаточно жесткой, чтобы не прогибаться под нагрузкой (значение E). Однако процесс определения размеров этих структурных элементов может быть сложным, если вы не инженер. Вот упрощенный подход, который поможет вам указать подходящий материал для многих приложений.
Первый шаг одинаков для пиломатериалов и конструктивных деревянных материалов: сложите все нагрузки, действующие на жатку или балку, а затем переведите эту нагрузку в термины , какую нагрузку будет ощущать каждый линейный фут жатки или балки .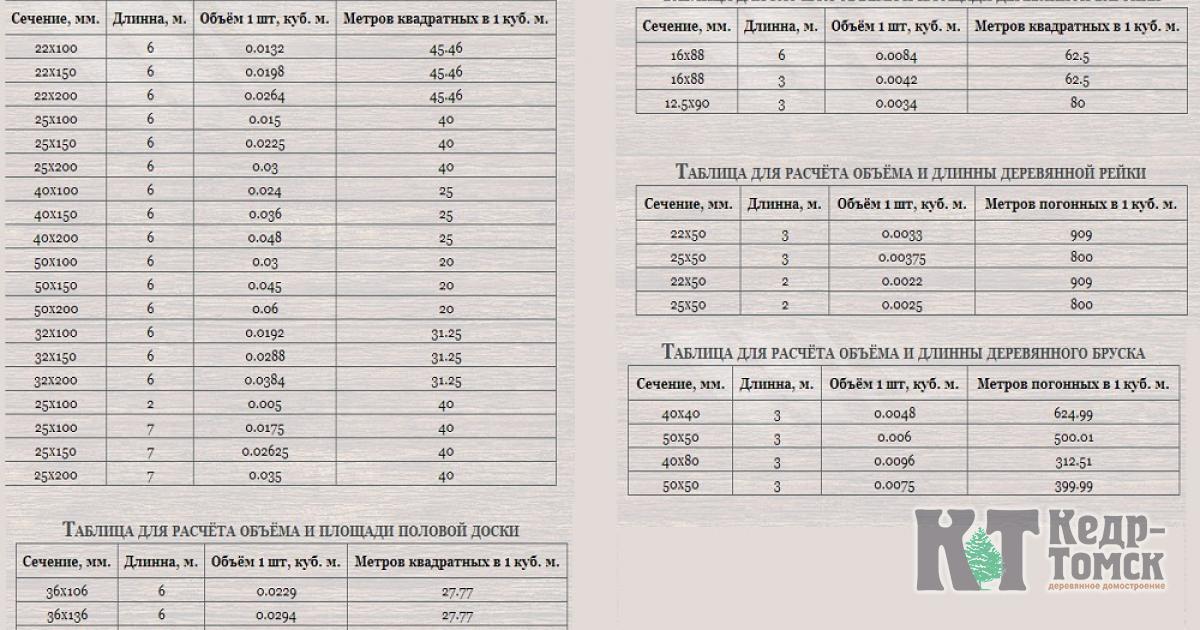 На языке луча вы говорите: этот заголовок должен нести Х-фунтов на линейный фут. Этот перевод является ключом к любой проблеме определения размеров конструкции. Вооружившись этой информацией, вы можете определить минимальный размер, пролет или прочность балки (кредит Хулио). Размеры компонентов из инженерной древесины определяются с помощью таблиц пролетов, которые сопоставляют различные пролеты с фунтами на фут балки. Для пиломатериалов необходимо выполнить математические расчеты.
На языке луча вы говорите: этот заголовок должен нести Х-фунтов на линейный фут. Этот перевод является ключом к любой проблеме определения размеров конструкции. Вооружившись этой информацией, вы можете определить минимальный размер, пролет или прочность балки (кредит Хулио). Размеры компонентов из инженерной древесины определяются с помощью таблиц пролетов, которые сопоставляют различные пролеты с фунтами на фут балки. Для пиломатериалов необходимо выполнить математические расчеты.
Нагрузки считаются либо распределенными , либо точечными нагрузками. Слой песка, равномерно распределенный по поверхности, является примером чистой распределенной нагрузки. Каждый квадратный метр поверхности испытывает одинаковую нагрузку. Живые и статические нагрузки, указанные в строительных нормах и правилах для крыш и полов, являются приближенными значениями распределенных нагрузок. Точечные нагрузки возникают, когда вес возлагается на одно место в конструкции, например на колонну. Нагрузка не распределяется поровну между опорной конструкцией. Анализ точечной нагрузки лучше оставить инженерам. Мы будем рассматривать только распределенные нагрузки. Это позволит нам подобрать размеры балок для наиболее распространенных применений.
Нагрузка не распределяется поровну между опорной конструкцией. Анализ точечной нагрузки лучше оставить инженерам. Мы будем рассматривать только распределенные нагрузки. Это позволит нам подобрать размеры балок для наиболее распространенных применений.
Рисунок 1
Проследим распределенные нагрузки для нескольких разных домов. Предположим, что все они расположены в одном и том же климате, но имеют разные пути загрузки из-за того, как они построены. Эти примеры иллюстрируют, как распределенные нагрузки назначаются конструктивным элементам. Наши образцы домов находятся в районе, где снеговая нагрузка составляет 50 фунтов на квадратный фут площади крыши (рассматривайте снег как динамическую нагрузку). Само собой разумеется, что в более теплом климате снеговая нагрузка, вероятно, будет меньше, поэтому вам необходимо проверить свою кодовую книгу на наличие постоянных и постоянных нагрузок в вашем регионе. Все нагрузки указаны в фунтах на квадратный фут горизонтальной проекции (площади опоры).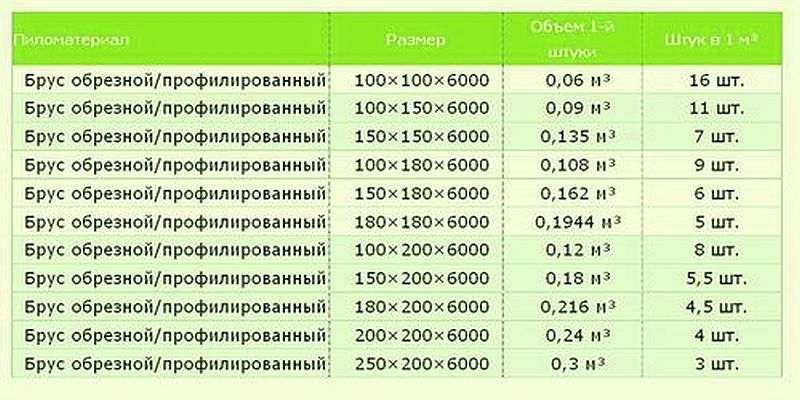 (СМ. РИСУНОК 1) 9Рис. 2 статическая нагрузка (всего 65 фунтов на квадратный фут) на конструкцию система поддержки. Помните, эти нагрузки распределяются равномерно по всей поверхности крыши. Внешняя стена (и перемычки внутри) будут нести все нагрузки от середины дома (между опорными стенами) к внешней стороне дома (включая свес крыши). Расстояние в этом случае составляет 12 футов + 2 фута = 14 футов. Таким образом, каждый линейный фут стены должен нести нагрузки, создаваемые полосой шириной 1 фут в этой области 14 футов. С технической точки зрения, ширина притока стены составляет 14 футов. Из этого мы можем легко увидеть, что каждый линейный фут стены поддерживает:
(СМ. РИСУНОК 1) 9Рис. 2 статическая нагрузка (всего 65 фунтов на квадратный фут) на конструкцию система поддержки. Помните, эти нагрузки распределяются равномерно по всей поверхности крыши. Внешняя стена (и перемычки внутри) будут нести все нагрузки от середины дома (между опорными стенами) к внешней стороне дома (включая свес крыши). Расстояние в этом случае составляет 12 футов + 2 фута = 14 футов. Таким образом, каждый линейный фут стены должен нести нагрузки, создаваемые полосой шириной 1 фут в этой области 14 футов. С технической точки зрения, ширина притока стены составляет 14 футов. Из этого мы можем легко увидеть, что каждый линейный фут стены поддерживает:
Условия:
динамическая нагрузка (снег): | 50 фунтов на квадратный фут x 14 футов = 700 фунтов на линейный фут |
Статическая нагрузка на крышу: | 15 фунтов на квадратный фут x 14 футов = 210 фунтов на линейный фут |
общая загрузка: | = 910 фунтов на погонный фут |
Важно перечислять динамическую нагрузку, стационарную нагрузку и общую нагрузку отдельно, поскольку динамическая нагрузка используется для расчета жесткости, а общая нагрузка используется для расчета прочности.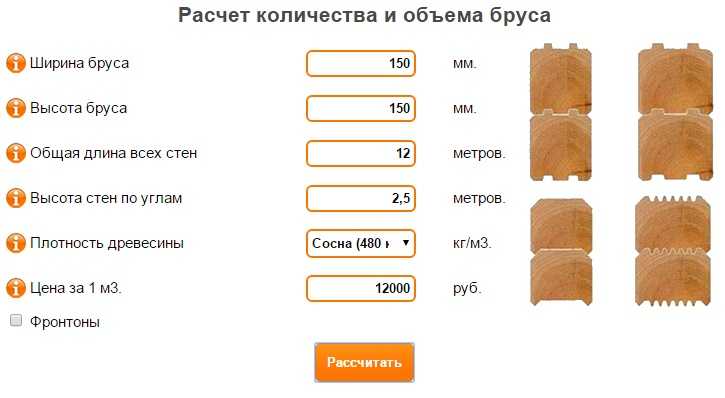
Рисунок 3
Пример #2
Этот дом идентичен нашему первому примеру, за исключением того, что он построен из палочек. В результате динамическая нагрузка, статическая нагрузка и распределение усилий различны. В отличие от стропильной крыши, временная и статическая нагрузки стропил и потолочных балок должны учитываться как отдельные системы. Поскольку чердак можно использовать для хранения, временная нагрузка на мансардный этаж устанавливается в соответствии с нормами 20 фунтов на квадратный фут.
Условия:
динамическая нагрузка (снег): | 50 фунтов на квадратный фут x 14 футов = 700 фунтов на линейный фут |
Статическая нагрузка на крышу: | 10 фунтов на квадратный фут x 14 футов = 140 фунтов на линейный фут |
живая нагрузка потолка: | 20 фунтов на квадратный фут x 6 футов = 120 фунтов на линейный фут |
статическая нагрузка на потолок: | 10 фунтов на квадратный фут x 6 футов = 60 фунтов на линейный фут |
общая загрузка: | = 1020 фунтов на погонный фут |
Рисунок 4
Пример верхнего колонтитула №3
Опять же, этот дом имеет ту же ширину, но имеет 2 уровня. На нижний коллектор действуют нагрузки от кровли, верхних стен и системы второго этажа. В Стандартах архитектурной графики вес внешней стены 2×6 указан как 16 фунтов на фут 9 .0297 2 . Таким образом, стена высотой 8 футов весит 8 футов x 16 фунтов/фут 2 = 128 фунтов на линейный фут. Грузы, доставленные в жатку:
На нижний коллектор действуют нагрузки от кровли, верхних стен и системы второго этажа. В Стандартах архитектурной графики вес внешней стены 2×6 указан как 16 фунтов на фут 9 .0297 2 . Таким образом, стена высотой 8 футов весит 8 футов x 16 фунтов/фут 2 = 128 фунтов на линейный фут. Грузы, доставленные в жатку:
Условия:
динамическая нагрузка (снег): | 50 фунтов на квадратный фут x 14 футов = 700 фунтов на линейный фут |
Статическая нагрузка на крышу: | 15 фунтов на квадратный фут x 14 футов = 210 фунтов на линейный фут |
стена верхнего уровня: | = 128 фунтов на линейный фут |
Временная нагрузка 2-го этажа: | 30 фунтов на квадратный фут x 6 футов = 180 фунтов на линейный фут |
Постоянная нагрузка 2-го этажа: | 10 фунтов на квадратный фут x 6 футов = 60 фунтов на линейный фут |
общая загрузка: | = 1278 фунтов на погонный фут |
Балки
Пример коньковой балки
Рисунок 5. На этом рисунке показаны 2 конструктивных элемента: коньковая балка и центральная балка. Оба имеют площадь притока 12 футов 0 дюймов. Нагрузка на фут балки определяется так же, как и для жаток.
На этом рисунке показаны 2 конструктивных элемента: коньковая балка и центральная балка. Оба имеют площадь притока 12 футов 0 дюймов. Нагрузка на фут балки определяется так же, как и для жаток.
Условия коньковой балки
динамическая нагрузка (снег): | 50 фунтов на квадратный фут x 12 футов = 600 фунтов на линейный фут |
статическая нагрузка на крышу: | 10 фунтов на квадратный фут x 12 футов = 120 фунтов на линейный фут |
общая загрузка: | = 720 фунтов на погонный фут |
Пример балки
Центральная балка несет половину нагрузки на перекрытие, нагрузку на перегородку и половину нагрузки на второй этаж. Живая и статическая нагрузки указаны в строительных нормах.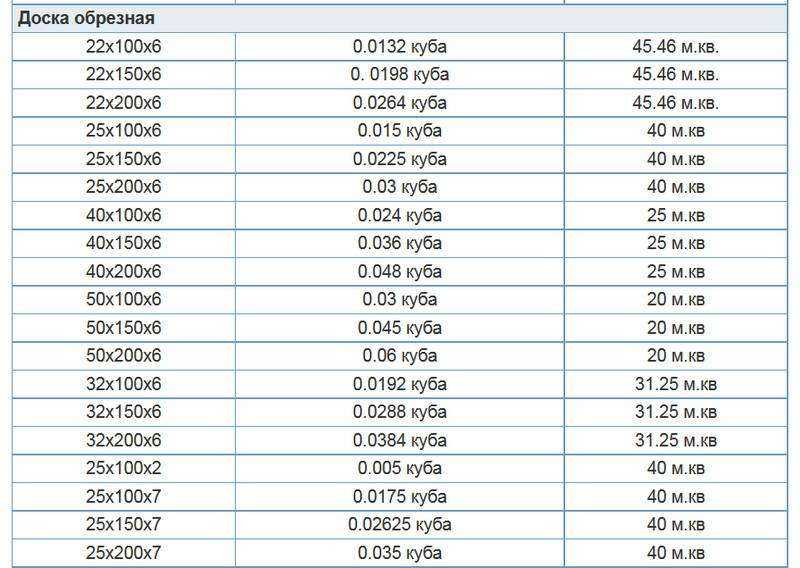 Вес перегородки указан в Стандартах архитектурной графики как 10 фунтов на квадратный фут.
Вес перегородки указан в Стандартах архитектурной графики как 10 фунтов на квадратный фут.
B) Состояние балки первого этажа
Временная нагрузка 1-го этажа: | 40 фунтов на квадратный фут x 12 футов = 480 фунтов на линейный фут |
Статическая нагрузка 1-го этажа: | 10 фунтов на квадратный фут x 12 футов = 120 фунтов на линейный фут |
Перегородка высотой 8 футов: | = 80 фунтов на линейный фут |
2-й этаж Временная нагрузка: | 30 фунтов на квадратный фут x 12 футов = 360 фунтов на линейный фут |
Постоянная нагрузка 2-го этажа: | 10 фунтов на квадратный фут x 12 футов = 120 фунтов на линейный фут |
общая загрузка: | = 1160 фунтов на погонный фут |
Резюме
Эти примеры являются типичными для типов расчетов, которые вам придется выполнять для определения равномерной нагрузки, распределяемой на балку или перемычку. Вы должны установить, какую нагрузку получает каждый линейный фут жатки или балки. Следующим шагом является использование технической литературы любой из компаний, производящих инженерные деревянные компоненты, для определения размера пролета и балки. Все они соотносят допустимые пролеты для нагрузки на фут балки. Списки пролетов основаны на допустимом отклонении, динамической нагрузке и статической нагрузке, которые перечислены в вашей книге строительных норм и правил. В части 2 «Определение размеров инженерных перекрытий и балок» мы сравниваем стоимость и характеристики некоторых изделий из инженерной древесины с пиломатериалами.
Вы должны установить, какую нагрузку получает каждый линейный фут жатки или балки. Следующим шагом является использование технической литературы любой из компаний, производящих инженерные деревянные компоненты, для определения размера пролета и балки. Все они соотносят допустимые пролеты для нагрузки на фут балки. Списки пролетов основаны на допустимом отклонении, динамической нагрузке и статической нагрузке, которые перечислены в вашей книге строительных норм и правил. В части 2 «Определение размеров инженерных перекрытий и балок» мы сравниваем стоимость и характеристики некоторых изделий из инженерной древесины с пиломатериалами.
Все иллюстрации предоставлены Journal of Light Construction.
Поиск:
Исследование в BCT
- MAJOR IN BCT (BS)
- ПРОФЕССИОНАЛЬНЫЙ МС
- ИССЛЕДОВАНИЯ MS И PHD
- ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАНИЕ
- СЕРТИФИКАТ ВЫПУСКНИКА
Присоединяйтесь к нашим информационным сессиям
Нет предстоящих событий.
 м
м
