Содержание
Формулы площади. Площадь треугольника, квадрата, прямоугольника, ромба, параллелограмма, трапеции, круга, эллипса.
Формулы площади. Площадь треугольника, квадрата, прямоугольника, ромба, параллелограмма, трапеции, круга, эллипса.
Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Онлайн калькуляторы для вычисления площадей плоских фигур
Формулы площади треугольника
Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высотыS = 1 a · h 2 Формула площади треугольника по трем сторонам
Формула Герона
S = √p(p — a)(p — b)(p — c)Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.
S = 1 a · b · sin γ 2 S = 1 a · c · sin β 2 S = 1 b · c · sin α 2 Формула площади треугольника по трем сторонам и радиусу описанной окружности
S = a · b · с 4R Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.S = p · r
где S — площадь треугольника,
a, b, c — длины сторон треугольника,
h — высота треугольника,
γ — угол между сторонами a и b,
r — радиус вписанной окружности,
R — радиус описанной окружности,p = a + b + c — полупериметр треугольника. 
2
Вы можете воспользоваться онлайн калькулятором для расчета площади треугольника.
Формулы площади квадрата
Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.S = a2
Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.S = 1 d2 2
где S — площадь квадрата,
a — длина стороны квадрата,
d — длина диагонали квадрата.
Вы можете воспользоваться онлайн калькулятором для расчета площади квадрата.
Формулы площади параллелограмма
Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.
S = a · h
Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.S = a · b · sin α
Формула площади параллелограмма по двум диагоналям и углу между ними
Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.S = 1 d1d2 sin γ 2
где S — Площадь параллелограмма,
a, b — длины сторон параллелограмма,
h — длина высоты параллелограмма,
d1, d2 — длины диагоналей параллелограмма,
α — угол между сторонами параллелограмма,
γ — угол между диагоналями параллелограмма.
Вы можете воспользоваться онлайн калькулятором для расчета площади параллелограмма.
Формулы площади ромба
Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.S = a · h
Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.S = a2 · sin α
Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей.S = 1 d1 · d2 2
где S — Площадь ромба,
a — длина стороны ромба,
h — длина высоты ромба,
α — угол между сторонами ромба,
d1, d2 — длины диагоналей.
Вы можете воспользоваться онлайн калькулятором для расчета площади ромба.
Формулы площади трапеции
Формула Герона для трапеции
S = a + b √(p-a)(p-b)(p-a-c)(p-a-d) |a — b| Формула площади трапеции по длине основ и высоте
Площадь трапеции равна произведению полусуммы ее оснований на высотуS = 1 (a + b) · h 2
где S — площадь трапеции,
a, b — длины основ трапеции,
c, d — длины боковых сторон трапеции,p = a + b + c + d — полупериметр трапеции. 2
Вы можете воспользоваться онлайн калькулятором для расчета площади трапеции.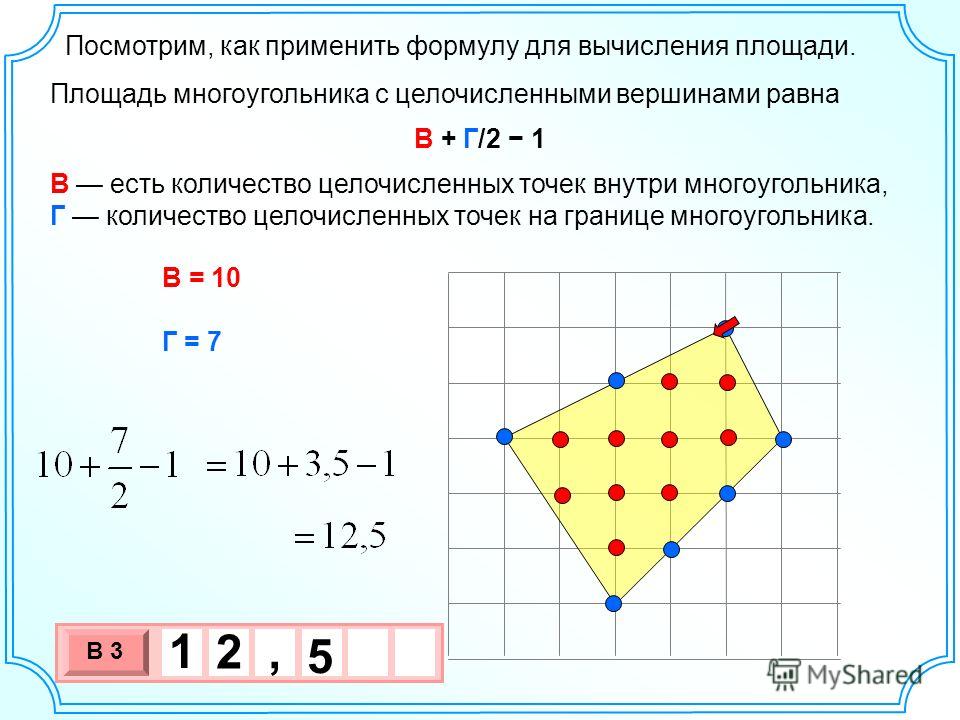
Формулы площади выпуклого четырехугольника
Формула площади четырехугольника по длине диагоналей и углу между ними
Площадь выпуклого четырехугольника равна половине произведения его диагоналей умноженному на синус угла между ними:
S = 1 d1 d2 sin α 2
где S — площадь четырехугольника,
d1, d2 — длины диагоналей четырехугольника,
α — угол между диагоналями четырехугольника.Формула площади описанного четырехугольника (по длине периметра и радиусу вписанной окружности)
Площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной окружности
S = p · r
-
Формула площади четырехугольника по длине сторон и значению противоположных углов
S = √(p — a)(p — b)(p — c)(p — d) — abcd cos2θ
где S — площадь четырехугольника,a, b, c, d — длины сторон четырехугольника,
p = a + b + c + d2 — полупериметр четырехугольника,
θ = α + β2 — полусумма двух противоположных углов четырехугольника.

-
Формула площади четырехугольника, вокруг которого можно описать окружность
S = √(p — a)(p — b)(p — c)(p — d)
Вы можете воспользоваться онлайн калькулятором для расчета площади четырехугольника.
Формулы площади круга
Формула площади круга через радиус
Площадь круга равна произведению квадрата радиуса на число пи.S = π r2
Формула площади круга через диаметр
Площадь круга равна четверти произведения квадрата диаметра на число пи.S = 1 π d2 4
где S — Площадь круга,
r — длина радиуса круга,
d — длина диаметра круга.
Вы можете воспользоваться онлайн калькулятором для расчета площади круга.
Все таблицы и формулы
Площадь прямоугольника как найти
Площадь прямоугольника очень часто требуется найти в задачах по геометрии. И не только — в повседневной жизни очень многие плоскости имеют форму прямоугольника и надо найти площадь прямоугольника. Как это сделать? Давайте рассмотрим все формулы и примеры.
Мы учимся вычислять площадь прямоугольника или площадь прямоугольника в школе. Однако, когда вы станете старше, вполне возможно, что вы не будете помнить, как найти площадь прямоугольника. Для начала давайте вспомним, что такое прямоугольник.
Содержание
Что такое прямоугольник
Давайте не будем «срезать углы». Чтобы иметь возможность вычислить площадь прямоугольника, естественно, что мы сначала знаем, что это такое. Поэтому для начала необходимо помнить, что прямоугольник является четырехугольником. Другими словами, это геометрическая фигура, которая имеет четыре стороны и четыре прямых угла. Противоположные стороны прямоугольника имеют одинаковую длину. Две самые длинные стороны представляют его длину, а две другие стороны представляют его ширину.
Две самые длинные стороны представляют его длину, а две другие стороны представляют его ширину.
Не все четырехугольники являются прямоугольниками. Действительно, обязательно, чтобы они имели следующие свойства, чтобы мы могли сказать, что это действительно прямоугольник:
Характеристики прямоугольника
Противоположные стороны должны быть параллельны.
- Диагонали прямоугольника должны быть одинаковой длины. Они также пересекаются в своей середине.
- Точка пересечения диагоналей прямоугольника называется центром симметрии.
- Кроме того, прямоугольник также является параллелограммом, так как его стороны попарно параллельны. Однако это частный случай параллелограмма. На самом деле он имеет четыре прямых угла, и его две параллельные стороны не должны иметь одинаковую длину. В противном случае все четыре стороны имеют одинаковую длину — тогда мы говорим о квадрате.
Формула площади прямоугольника
Как рассчитать площадь прямоугольника? Обратите внимание, что базовую формулу для вычисления площади (или площади) прямоугольника очень легко запомнить. Вы просто должны умножить его длину на ширину.
Вы просто должны умножить его длину на ширину.
Площадь прямоугольника равна его длине, умноженной на ширину.
Например, площадь прямоугольника длиной 4 сантиметра и шириной 2 сантиметра равна 4 x 2 = 8 см².
Найти площадь прямоугольника по известным длине и ширине — онлайн калькулятор.
Введите длину a:
Введите ширину b:
Площадь прямоугольника:
Диагональ прямоугольника:
Площадь поверхности прямоугольника длиной L и шириной l равна: S = L x l
Принцип расчета площади прямоугольника
Чтобы вычислить площадь прямоугольника, мы посчитаем количество единиц областей, которые содержит прямоугольник:
В прямоугольнике выше 12 квадратов по 1 см². Его площадь составляет 12 см² (4 х 3).
Примечание. В этом расчете длина L и ширина l прямоугольника должны быть выражены в одной и той же единице длины. Результат будет выражен в той же единице измерения, возведенной в квадрат. Например, если длина прямоугольника выражена в метрах, ширина также должна быть выражена в метрах, а результат формулы для расчета площади прямоугольника даст результат в квадратных метрах (м²).
Площадь прямоугольника эквивалентна его территории. Территория — это термин, используемый для обозначения меры площади земли (мы используем единицу измерения гектар, а не м²). Гектар — это метрическая мера земельной площади, равная 10 000 м2.
Пример расчета
Рассмотрим прямоугольник длиной L = 4 см и шириной l = 2 см. Площадь S его поверхности равна:
A = L x l = 4 x 2 = 8 см².
Как рассчитать площадь прямоугольника, если мы знаем только одну сторону и диагональ
Можно определить площадь прямоугольника другим способом. Формула, которая была изложена ранее, не является единственным методом, который можно использовать. Действительно, вполне возможно сделать это по-другому. Для этого нам нужно будет, по крайней мере, измерить только одну сторону и необходимо знать длину диагонали. В этом случае мы делаем расчет, используя теорему Пифагора.
Что такое теорема Пифагора
Это формула, которая используется для определения длины третьей стороны прямоугольного треугольника, когда вы уже знаете значение двух других его сторон.
Обратите внимание, что прямоугольник состоит из двух прямоугольных треугольников. Действительно, диагональ представляет гипотенузу этого типа треугольника.
Теорема Пифагора
Кроме того, это также самая длинная сторона, которую можно найти на рисунке. Длина и ширина, с другой стороны, представляют две другие его стороны (скажем, смежные стороны). Это причина, почему можно использовать эту формулу для определения площади прямоугольника.
Теорема Пифагора основана на довольно простом уравнении, которое выглядит следующим образом: a² + b² = c². Где a и b используются для представления двух соседних сторон — катетов прямоугольного треугольника, а c представляет гипотенузу треугольника.
Чтобы полностью понять использование этой формулы, мы начнем с очень конкретного примера. Для этого предположим, что диагональ прямоугольника 10 см, а другая сторона 6 см. Если мы ссылаемся на формулу a² + b² = c², следовательно, сторона «a» составляет 6 см, а гипотенуза «c» — 10 см. Теперь нам нужно просто заменить буквенные значения числовыми значениями, которые у нас есть. Что дает нам:
Теперь нам нужно просто заменить буквенные значения числовыми значениями, которые у нас есть. Что дает нам:
a² + b² = c²
6² + b² = 10²
b² = 10² — 6²
b² = 100 — 36
b² = 64
b= 8
Мы получаем длину смежной стороны прямоугольника «b», которая равна 8 см. Теперь мы можем рассчитать площадь прямоугольника:
S = 8 см х 6 см
Следовательно, S = 48 см².
Вычисление площади | SkillsYouNeed
Площадь — это мера того, сколько места внутри фигуры. Вычисление площади формы или поверхности может быть полезно в повседневной жизни — например, вам может понадобиться знать, сколько краски нужно купить, чтобы покрыть стену, или сколько семян травы вам нужно, чтобы посеять газон.
На этой странице собрана основная информация, которую вам необходимо знать, чтобы понимать и вычислять площади обычных фигур, включая квадраты и прямоугольники, треугольники и круги.
Расчет площади методом сетки
Когда фигура рисуется на масштабированной сетке, вы можете найти площадь, подсчитав количество квадратов сетки внутри фигуры.
В этом примере внутри прямоугольника 10 квадратов сетки.
Чтобы найти значение площади с помощью метода сетки, нам нужно знать размер, который представляет квадрат сетки.
В этом примере используются сантиметры, но тот же метод применим для любой единицы длины или расстояния. Например, вы можете использовать дюймы, метры, мили, футы и т. д.
В этом примере каждый квадрат сетки имеет ширину 1 см и высоту 1 см. Другими словами, каждый квадрат сетки равен одному «квадратному сантиметру».
Подсчитайте квадраты сетки внутри большого квадрата, чтобы найти его площадь.
Имеется 16 маленьких квадратов, поэтому площадь большого квадрата составляет 16 квадратных сантиметров.
В математике квадратные сантиметры сокращаются до см 2 . 2 означает «квадратный».
Каждый квадрат сетки равен 1 см 2 .
Площадь большого квадрата 16см 2 .
Подсчет квадратов на сетке для нахождения площади работает для всех фигур, если известны размеры сетки. Однако этот метод становится более сложным, когда фигуры не точно соответствуют сетке или когда вам нужно подсчитать доли квадратов сетки.
Однако этот метод становится более сложным, когда фигуры не точно соответствуют сетке или когда вам нужно подсчитать доли квадратов сетки.
В этом примере квадрат не вписывается точно в сетку.
Мы все еще можем вычислить площадь, считая квадраты сетки.
- Имеется 25 полных квадратов сетки (заштрихованы синим цветом).
- 10 половинных квадратов сетки (заштрихованы желтым цветом) – 10 половинных квадратов соответствуют 5 полным квадратам.
- Также есть 1 четверть квадрата (заштриховано зеленым цветом) – (¼ или 0,25 целого квадрата).
- Сложите целые квадраты и дроби вместе: 25 + 5 + 0,25 = 30,25.
Следовательно, площадь этого квадрата равна 30,25 см 2 .
Вы также можете записать это как 30¼cm 2 .
Хотя использование сетки и подсчет квадратов внутри формы является очень простым способом изучения понятий площади, он менее полезен для нахождения точных площадей с более сложными формами, когда может быть много долей квадратов сетки, которые нужно сложить вместе.
Площадь можно рассчитать с помощью простых формул, в зависимости от типа фигуры, с которой вы работаете.
Оставшаяся часть этой страницы объясняет и дает примеры того, как вычислить площадь фигуры без использования системы сетки.
Площади простых четырехугольников:
Квадраты, прямоугольники и параллелограммы
Простейшие (и наиболее часто используемые) вычисления площадей предназначены для квадратов и прямоугольников.
Чтобы найти площадь прямоугольника, умножьте его высоту на ширину.
Площадь прямоугольника = высота × ширина
Для квадрата вам нужно только найти длину одной из сторон (поскольку каждая сторона имеет одинаковую длину), а затем умножить это само на себя, чтобы найти площадь. Это то же самое, что сказать длину 2 или длина в квадрате.
Хорошей практикой является проверка того, что фигура на самом деле является квадратом, путем измерения двух сторон. Например, стена комнаты может выглядеть как квадрат, но когда вы ее измерите, вы обнаружите, что на самом деле это прямоугольник.
Часто в реальной жизни формы могут быть более сложными. Например, представьте, что вы хотите найти площадь пола, чтобы заказать нужное количество ковра.
Типовой план помещения не может состоять из простого прямоугольника или квадрата:
В этом и других подобных примерах хитрость заключается в том, чтобы разбить фигуру на несколько прямоугольников (или квадратов). Неважно, как вы разделите фигуру — любое из трех решений приведет к одному и тому же ответу.
Решение 1 и 2 требуют, чтобы вы сделали две фигуры и сложили их площади вместе, чтобы найти общую площадь.
Для решения 3 вы делаете большую фигуру (A) и вычитаете из нее меньшую фигуру (B), чтобы найти площадь.
Другая распространенная проблема заключается в том, чтобы найти область границы — фигура внутри другой фигуры.
В этом примере показан путь вокруг поля шириной 2 метра.
Опять же, в этом примере есть несколько способов определить площадь пути.
Вы можете рассматривать путь как четыре отдельных прямоугольника, вычислять их размеры, затем их площадь и, наконец, складывать площади вместе, чтобы получить общую сумму.
Более быстрым способом было бы определить площадь всей фигуры и площадь внутреннего прямоугольника. Вычтите внутреннюю площадь прямоугольника из целого, оставив площадь пути.
- Площадь всей фигуры 16 м × 10 м = 160 м 2 .
- Мы можем рассчитать размеры средней секции, потому что знаем, что путь по краю имеет ширину 2 м.
- Ширина всей фигуры 16 м, а ширина пути по всей фигуре 4 м (2 м слева от фигуры и 2 м справа). 16м — 4м = 12м
- То же самое можно сделать для высоты: 10 м — 2 м — 2 м = 6 м
- Итак, мы подсчитали, что средний прямоугольник имеет размеры 12 м × 6 м.
- Таким образом, площадь среднего прямоугольника равна: 12 м × 6 м = 72 м 2 .
- Наконец, мы отделяем площадь среднего прямоугольника от площади всей фигуры. 160 — 72 = 88м 2 .
Площадь пути 88 м 2 .
A Параллелограмм — это четырехсторонняя фигура с двумя парами сторон одинаковой длины — по определению прямоугольник — это разновидность параллелограмма. Однако большинство людей склонны думать о параллелограммах как о четырехгранных фигурах с наклонными линиями, как показано здесь.
Однако большинство людей склонны думать о параллелограммах как о четырехгранных фигурах с наклонными линиями, как показано здесь.
Площадь параллелограмма вычисляется так же, как и для прямоугольника (высота × ширина), но важно понимать, что под высотой понимается не длина вертикальных (или не вертикальных) сторон, а расстояние между сторонами .
Из диаграммы видно, что высота — это расстояние между верхней и нижней сторонами фигуры, а не длина стороны.
Представьте воображаемую линию под прямым углом между верхней и нижней сторонами. Это высота.
Вычисление площади треугольников
Треугольник можно представить как половину квадрата или параллелограмма.
Предполагая, что вы знаете (или можете измерить) размеры треугольника, вы можете быстро вычислить его площадь, используя следующую формулу:
Площадь треугольника = (высота × ширина) ÷ 2.
Другими словами, вы можете вычислите площадь треугольника так же, как площадь квадрата или параллелограмма, а затем просто разделите ответ на 2.
Высота треугольника измеряется как прямоугольная линия от нижней линии (основания) до «вершины» (верхней точки) треугольника.
Вот несколько примеров:
Площадь трех треугольников на диаграмме выше одинакова.
Каждый треугольник имеет ширину и высоту 3 см.
Площадь вычисляется:
(высота × ширина) ÷ 2
3 × 3 = 9
9 ÷ 2 = 4,5
Площадь каждого треугольника равна 4,5 см 2 .
В реальных ситуациях вы можете столкнуться с задачей, требующей нахождения площади треугольника, например:
Вы хотите покрасить фронтон сарая. Вы только хотите посетить отделочный магазин один раз, чтобы получить нужное количество краски. Вы знаете, что литр краски покроет 10м 2 стены. Сколько краски нужно, чтобы покрыть фронтон?
Вам нужно три измерения:
A — Общая высота до вершины крыши.
B — Высота вертикальных стен.
C — Ширина здания.
В этом примере размеры:
A — 12,4 м
B — 6,6 м
C — 11,6 м
Следующий этап требует дополнительных расчетов. Думайте о здании как о двух формах, прямоугольнике и треугольнике. По имеющимся у вас измерениям вы можете рассчитать дополнительные измерения, необходимые для определения площади конца фронтона.
Измерение D = 12,4 — 6,6
D = 5,8 м
Теперь вы можете разрабатывать площадь двух частей стены:
Площадь прямоугольной части стены: 6,6 × 11 = 76,56 м. 2
Площадь треугольной части стены: (5,8 × 11,6) ÷ 2 = 33,64 м 2
Сложите эти две площади вместе, чтобы найти общую площадь:
76,56 + 33,64 = 110,2 м 2
Как известно, один литр краски покрывает 10 м 2 стены, чтобы мы могли вычислить, сколько литров нам нужно купить:
110,2 ÷ 10 = 11,02 литра.
На самом деле вы можете обнаружить, что краска продается только в 5-литровых или 1-литровых банках, в результате получается чуть более 11 литров. У вас может возникнуть соблазн округлить до 11 литров, но если мы не разбавим краску водой, этого будет недостаточно. Таким образом, вы, вероятно, округлите до следующего целого литра и купите две 5-литровые банки и две 1-литровые банки, что в сумме составит 12 литров краски. Это позволит избежать любых потерь и оставит большую часть литра для подкрашивания позже. И не забывайте, если вам нужно нанести более одного слоя краски, вы должны умножить количество краски на один слой на необходимое количество слоев!
У вас может возникнуть соблазн округлить до 11 литров, но если мы не разбавим краску водой, этого будет недостаточно. Таким образом, вы, вероятно, округлите до следующего целого литра и купите две 5-литровые банки и две 1-литровые банки, что в сумме составит 12 литров краски. Это позволит избежать любых потерь и оставит большую часть литра для подкрашивания позже. И не забывайте, если вам нужно нанести более одного слоя краски, вы должны умножить количество краски на один слой на необходимое количество слоев!
Площади кругов
Для вычисления площади круга необходимо знать его диаметр или радиус .
Диаметр окружности — это длина прямой линии от одной стороны окружности до другой, проходящей через центральную точку окружности. Диаметр в два раза больше длины радиуса (диаметр = радиус × 2)
Радиус окружности — это длина прямой линии от центральной точки окружности до ее края.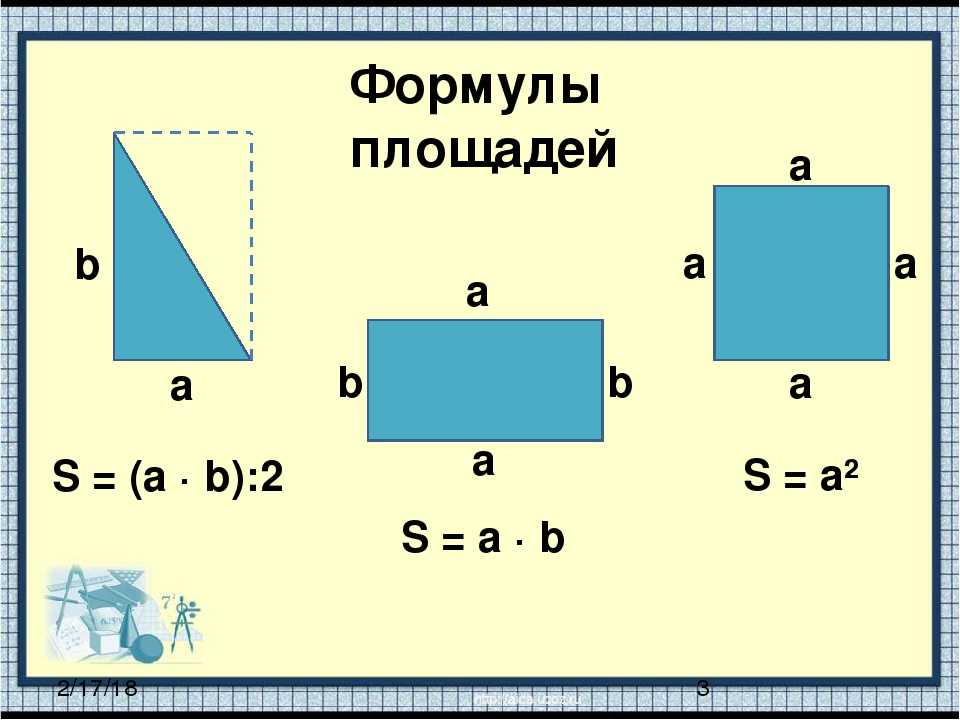 Радиус равен половине диаметра. (радиус = диаметр ÷ 2)
Радиус равен половине диаметра. (радиус = диаметр ÷ 2)
Вы можете измерить диаметр или радиус в любой точке окружности – важно измерять с помощью прямой линии, которая проходит через (диаметр) или заканчивается (радиус) в центре окружности.
На практике при измерении окружностей часто бывает проще измерить диаметр, чем разделить его на 2, чтобы найти радиус.
Радиус нужен для вычисления площади круга, формула такова:
Площадь круга = πR 2 .
Это означает:
π = Pi — константа, равная 3,142.
R = радиус окружности.
R 2 (радиус в квадрате) означает радиус × радиус.
Следовательно, круг с радиусом 5 см имеет площадь:
3,142 × 5 × 5 = 78,55 см 2 .
Круг диаметром 3м имеет площадь:
Сначала вычисляем радиус (3м ÷ 2 = 1,5м)
Затем применяем формулу:
πR 2
3,142 × 1,5 × 1,5 = 7,0695.
Площадь круга диаметром 3 м равна 7,0695 м 2 .
Заключительный пример
Этот пример использует большую часть содержимого этой страницы для решения простых задач с площадями.
Это дом Рубена М. Бенджамина в Блумингтоне, штат Иллинойс, внесенный в Национальный реестр исторических мест США (регистрационный номер: 376599).
Этот пример включает в себя нахождение площади фасада дома, деревянной решетчатой части, исключая дверь и окна. Вам нужны следующие мерки:
| А – 9,7 м | В – 7,6 м |
| С – 8,8 м | Г – 4,5 м |
| В – 2,3 м | В – 2,7 м |
| Г – 1,2 м | В – 1,0 м |
Примечания:
- Все измерения являются приблизительными.
- О бордюре вокруг дома можно не беспокоиться – он не учитывался при измерениях.
- Мы предполагаем, что все прямоугольные окна имеют одинаковый размер.

- Размер круглого окна — это диаметр окна.
- Размеры двери включают ступени.
Какова площадь деревянной решетчатой части дома?
Вычисления и ответы ниже:
Ответы на приведенный выше пример
Сначала вычислите площадь основной формы дома – прямоугольника и треугольника, составляющих фигуру.
Основной прямоугольник (В × С) 7,6 × 8,8 = 66,88м 2 .
Высота треугольника (A – B) 9,7 – 7,6 = 2,1.
Следовательно, площадь треугольника равна (2,1 × C) ÷ 2,
2,1 × 8,8 = 18,48. 18,48 ÷ 2 = 9,24 м 2 .
Суммарная полная площадь фасада дома равна сумме площадей прямоугольника и треугольника:
66,88 + 9,24 = 76,12 м 2 .
Затем определите площади окон и дверей, чтобы их можно было вычесть из общей площади.
Площадь двери и ступеней составляет (D × E) 4,5 × 2,3 = 10,35 м 2 .
Площадь одного прямоугольного окна составляет (G × F) 1,2 × 2,7 = 3,24 м 2 .
Пять прямоугольных окон. Умножьте площадь одного окна на 5.
3,24 × 5 = 16,2 м2. (общая площадь прямоугольных окон).
Круглое окно имеет диаметр 1 м, поэтому его радиус равен 0,5 м.
Используя πR 2 , определите площадь круглого окна: 3,142 × 0,5 × 0,5 =. 0,7855 м 2 .
Затем добавьте площади дверей и окон.
(площадь дверей) 10,35 + (площадь прямоугольных окон) 16,2 + (площадь круглых окон) 0,7855 = 27,3355
Наконец, вычтите общую площадь окон и дверей из полной площади.
76,12 – 27,3355 = 48,7845
Площадь деревянного реечного фасада дома, а ответ на задачу: 48,7845м 2 .
Вы можете округлить ответ до 48,8 м 2 или 49 м 2 .
См. нашу страницу по Оценка, приближение и округление .
Дальнейшее чтение из книги «Навыки, которые вам нужны»
Понимание геометрии
Часть руководства «Навыки, которые вам необходимы для счета»
В этой электронной книге рассматриваются основы геометрии и рассматриваются свойства фигур, линий и твердых тел. Эти концепции построены в книге, с примерами работы и возможностями для вас, чтобы попрактиковаться в ваших новых навыках.
Эти концепции построены в книге, с примерами работы и возможностями для вас, чтобы попрактиковаться в ваших новых навыках.
Если вы хотите освежить свои знания или помочь своим детям в обучении, эта книга для вас.
Формула площади. Что такое формулы площади для различных геометрических фигур?
Пространство или область, окруженная замкнутой геометрической фигурой в двумерной плоскости , называется областью. Кроме того, это количество, которое выражает протяженность двумерной фигуры или формы или плоской пластинки на плоскости. Формулы площади используются для расчета пространства, ограниченного различными геометрическими фигурами. Формулы геометрической площади применимы к правильным геометрическим фигурам, имеющим определенные размеры.
Что такое формулы площади?
Различные Формулы площади используются для вычисления площади различных геометрических фигур. Некоторые из важных геометрических фигур: квадрат, прямоугольник, круг, треугольник, трапеция, эллипс.
Формула площади для треугольника:
Площадь треугольника можно рассчитать, найдя половину произведения длины его основания и высоты. Формула площади треугольника задается как
Площадь треугольника = 1/2 × основание × высота
Формула площади для квадрата:
Площадь квадрата вычисляется путем нахождения квадрата длины каждой стороны квадрата. Формула площади квадрата задается следующим образом:
Площадь квадрата = сторона × сторона = сторона 2
Формула площади для круга:
Площадь круга можно вычислить, найдя произведение числа пи на квадрат радиуса. Формула площади круга дается как
Площадь круга = πr 2
Формула площади для прямоугольника:
Площадь прямоугольника вычисляется путем умножения длины и ширины прямоугольника. Формула площади прямоугольника задается следующим образом:
Площадь прямоугольника = длина × ширина
Формула площади для параллелограмма:
Площадь параллелограмма можно рассчитать, умножив основание и высоту параллелограмма. Формула площади параллелограмма задается как
Формула площади параллелограмма задается как
Площадь параллелограмма = основание × высота
Формула площади для ромба:
Площадь ромба можно вычислить, найдя половину произведения длин его диагоналей. Формула площади четырехугольника задается как половина произведения суммы параллельных сторон и высоты. Формула площади трапеции задается как
Площадь трапеции = 1/2 × сумма параллельных сторон (a + b) × высота (h)
Формула площади для эллипса:
Площадь эллипса – это произведение числа Пи на большую и малую оси. Формула площади эллипса задается следующим образом:
Площадь эллипса = π × Большая ось (a) × Малая ось (b)
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Закажите бесплатный пробный урок
Давайте изучим формулы геометрической площади для различных фигур, используя приведенные ниже примеры.
Примеры с использованием формулы геометрической площади
Пример 1: Какова площадь прямоугольного парка, длина и ширина которого равны 60 м и 90 м соответственно?
Решение:
Найти: Площадь прямоугольного парка.
Дано:
Длина парка = 60 м
Ширина парка = 90 м 0024 2
= 5400 м 2
Ответ: Площадь прямоугольного парка 5400 м 2 .
Пример 2 : Какова площадь круглого парка радиусом 400 м?
Решение:
Найти: площадь круглого парка.
Дано:
Радиус кругового парка = 400 м
Используя формулу площади,
Площадь круга = πr 2
Площадь круга = π 400 2
= 160000π м 2
Ответ: Площадь круглого парка 160000π м 2 .
Пример 3: Какова площадь квадрата, каждая сторона которого равна 5 единицам?
Решение:
Используя формулу площади для квадрата, мы имеем
Площадь = 5 × 5 = 25 квадратных единиц
Ответ: Площадь квадрата составляет 25 квадратных единиц.
Часто задаваемые вопросы о формулах площади
Что такое формулы площади?
Формулы площади используются для нахождения площади или области, охватываемой любой двумерной фигурой. Формула площади для нескольких фигур дается как
- Площадь квадрата = (сторона) 2
- Площадь прямоугольника = длина × ширина
- Площадь треугольника = (1/2) × основание × высота
Что такое формула площади для квадрата?
Формула площади для квадрата используется для нахождения площади, покрытой квадратом в 2-D плоскости. Формула площади квадрата задается следующим образом: площадь квадрата = (сторона) 9.0024 2 .
Какая формула площади прямоугольника?
Формула площади прямоугольника используется для нахождения площади, покрытой прямоугольником в двухмерной плоскости. Формула площади прямоугольника задается как Площадь прямоугольника = длина × ширина.
Каково применение формулы площади?
Формула площади находит применение при расчете общей области, охватываемой фигурой в 2-D плоскости.






