Мощность формула тока: Работа и мощность тока — урок. Физика, 8 класс.

Похожие материалы:

Добавить комментарий

Мощность электрического тока: формула

Прежде чем рассматривать электрическую мощность, следует определиться, что же представляет собой мощность вообще, как физическое понятие. Обычно, говоря об этой величине, подразумевается определенная внутренняя энергия или сила, которой обладает какой-либо объект. Это может быть мощность устройства, например, двигателя или действия (взрыв). Ее не следует путать с силой, поскольку это разные понятия.

Содержание

Что такое мощность электрического тока

Любые физические действия совершаются под влиянием силы. С ее помощью проделывается определенный путь, то есть выполняется работа. В свою очередь, работа А, проделанная в течение определенного времени t, составит значение мощности, выраженное формулой: N = A/t (Вт = Дж/с). Другое понятие мощности связано со скоростью преобразования энергии той или иной системы. Одним из таких преобразований является мощность электрического тока, с помощью которой также выполняется множество различных работ. В первую очередь она связана с электродвигателями и другими устройствами, выполняющими полезные действия.

Мощность тока связана сразу с несколькими физическими величинами. Напряжение (U) представляет собой работу, затрачиваемую на перемещение 1 кулона. Сила тока (I) соответствует количеству кулонов, проходящих за 1 секунду. Таким образом, ток, умноженный на напряжение (I x U), соответствует полной работе, выполненной за 1 секунду. Полученное значение и будет мощностью электрического тока.

Приведенная формула мощности тока показывает, что мощность находится в одинаковой зависимости от силы тока и напряжения. Отсюда следует, что одно и то же значение этого параметра можно получить за счет большого тока и малого напряжения и, наоборот, при высоком напряжении и малом токе. Это свойство позволяет передавать электроэнергию на дальние расстояния от источника к потребителям. В процессе передачи ток преобразуется с помощью трансформаторов, установленных на повышающих и понижающих подстанциях.

Существует два основных вида электрической мощности – активная и реактивная. В первом случае происходит безвозвратное превращение мощности электрического тока в механическую, световую, тепловую и другие виды энергии. Для нее применяется единица измерения – ватт. 1Вт = 1В х 1А. На производстве и в быту используются более крупные значения – киловатты и мегаватты.

К реактивной мощности относится такая электрическая нагрузка, которая создается в устройствах за счет индуктивных и емкостных колебаний энергии электромагнитного поля. В переменном токе эта величина представляет собой произведение, выраженное следующей формулой: Q = U х I х sin(угла). Синус угла означает сдвиг фаз между рабочим током и падением напряжения. Q является реактивной мощностью, измеряемой в Вар – вольт-ампер реактивный. Данные расчеты помогают эффективно решить вопрос, как найти мощность электрического тока, а формула, существующая для этого, позволяет быстро выполнить вычисления.

Обе мощности можно наглядно рассмотреть на простом примере. Какое-либо электротехническое устройство оборудовано нагревательными элементами – ТЭНами и электродвигателем. Для изготовления ТЭНов используется материал, обладающий высоким сопротивлением, поэтому при прохождении по нему тока, вся электрическая энергия преобразуется в тепловую. Данный пример очень точно характеризует активную электрическую мощность.

Что касается электродвигателя, то внутри него расположена медная обмотка, обладающая индуктивностью, которая, в свою очередь, обладает эффектом самоиндукции. Благодаря этому эффекту, происходит частичный возврат электричества обратно в сеть. Возвращаемая энергия характеризуется небольшим смещением в параметрах напряжения и тока, оказывая негативное влияние на электрическую сеть в виде дополнительных перегрузок.

Такие же свойства имеют и конденсаторы из-за своей электрической емкости, когда накопленный заряд отдается обратно. Здесь также смещаются значения тока и напряжения, только в противоположном направлении. Данная энергия индуктивности и емкости, со смещением по фазе относительно значений действующей электросети, как раз и есть реактивная электрическая мощность. Благодаря противоположному эффекту индуктивности и емкости в отношении сдвига фазы, становится возможным выполнить компенсацию реактивной мощности, повышая, тем самым, эффективность и качество электроснабжения.

По какой формуле вычисляется мощность электрического тока

Правильное и точное решение вопроса чему равна мощность электрического тока, играет решающую роль в деле обеспечения безопасной эксплуатации электропроводки, предупреждения возгораний из-за неправильно выбранного сечения проводов и кабелей. Мощность тока в активной цепи зависит от силы тока и напряжения. Для измерения силы тока существует прибор – амперметр. Однако не всегда возможно воспользоваться этим прибором, особенно когда проект здания еще только составляется, а электрической цепи просто не существует. Для таких случаев предусмотрена специальная методика проведения расчетов. Силу тока можно определить по формуле при наличии значений мощности, напряжения сети и характера нагрузки.

Существует формула мощности тока, применительно к постоянным значениям силы тока и напряжения: P = U x I. При наличии сдвига фаз между силой тока и напряжением, для расчетов используется уже другая формула: P = U x I х cos φ. Кроме того, мощность можно определить заранее путем суммирования мощности всех приборов, которые запланированы к вводу в эксплуатацию и подключению к сети. Эти данные имеются в технических паспортах и руководствах по эксплуатации устройств и оборудования.

Таким образом, формула определения мощности электрического тока позволяет вычислить силу тока для однофазной сети: I = P/(U x cos φ), где cos φ представляет собой коэффициент мощности. При наличии трехфазной электрической сети сила тока вычисляется по такой же формуле, только к ней добавляется фазный коэффициент 1,73: I = P/(1,73 х U x cos φ). Коэффициент мощности полностью зависит от характера планируемой нагрузки. Если предполагается использовать лишь лампы освещения или нагревательные приборы, то он будет составлять единицу.

При наличии реактивных составляющих в активных нагрузках, коэффициент мощности уже считается как 0,95. Данный фактор обязательно учитывается в зависимости от того, какой тип электропроводки используется. Если приборы и оборудование обладают достаточно высокой мощностью, то коэффициент составит 0,8. Это касается сварочных аппаратов, электродвигателей и других аналогичных устройств.

Для расчетов при наличии однофазного тока значение напряжения принимается 220 вольт. Если присутствует трехфазный ток, расчетное напряжение составит 380 вольт. Однако с целью получения максимально точных результатов, необходимо использовать в расчетах фактическое значение напряжения, измеренное специальными приборами.

От чего зависит мощность тока

Мощность тока, различных приборов и оборудования зависит сразу от двух основных величин – силы тока и напряжения. Чем выше ток, тем больше значение мощности, соответственно, при повышении напряжения, мощность также возрастает. Если напряжение и сила тока увеличиваются одновременно, то мощность электрического тока будет возрастать как произведение той и другой величины: N = I x U.

Очень часто возникает вопрос, в чем измеряется мощность тока? Основной единицей измерения этой величины является 1 ватт (Вт). Таким образом, 1 ватт является мощностью устройства, потребляющего ток силой в 1 ампер, при напряжении 1 вольт. Подобной мощностью обладает, например, лампочка от обычного карманного фонарика.

Расчетное значение мощности позволяет точно определить расход электрической энергии. Для этого необходимо взять произведение мощности и времени. Сама формула выглядит так: W = IUt где W является расходом электроэнергии, произведение IU – мощностью, а t – количеством отработанного времени. Например, чем больше продолжается работа электрического двигателя, тем большая работа им совершается. Соответственно возрастает и потребление электроэнергии.

Сопротивление току напряжения и электрическая мощность общие основные электрические формулы математические расчеты формула калькулятора для расчета мощности уравнение работы энергии закон мощности ватты понимание общая электрическая круговая диаграмма расчет электроэнергии электрическая ЭДС напряжение формула мощности уравнение два разных уравнения для расчета мощности общий закон ома аудио физика электричество электроника формула колесо формулы амперы ватты вольты омы уравнение косинуса аудиотехника круговая диаграмма заряд физика мощность звукозапись расчет электротехника формула мощность математика пи физика отношение отношение

Напряжение, ток, сопротивление и электрическая мощность, общие основные электрические формулы, математические расчеты, формула калькулятора для расчета мощности, энергия, работа, уравнение, мощность, закон, ватты, понимание, общая электрическая круговая диаграмма, расчет электричества, электрическая ЭДС, напряжение, формула мощности, уравнение, два разных уравнения для расчета мощности, общий закон Ома, аудиофизика, электричество, электроника. формула колесо формулы амперы ватты вольты омы уравнение косинуса аудиотехника круговая диаграмма заряд физика мощность звукозапись расчет электротехника формула мощность математика пи физика отношения отношения — sengpielaudio Sengpiel Berlin

Electric Current , Electric Power , Electrical Voltage
 
Electricity and Electric Charge
 
The most common general formulas used in electrical engineering
 
● Основные формулы and Calculations   ●
 
Relationship of the physical and electrical quantities (parameters)  
Electric voltage V , amperage I , resistivity
R , импеданс Z ,
мощность и мощность P
Вольт В , Ампер А,

8 сопротивление

Импеданс Ом ω и WATT W

Номинальный импеданс Z = 4, 8 и 16 Ом (Loudspeakers). Р . Уравнение закона Ома (формула): В = I × R и уравнение степенного закона (формула): P = I × В . P = мощность, I или J = латиница: influare, международный ампер или интенсивность и R = сопротивление. В = напряжение, разность электрических потенциалов Δ В или E = электродвижущая сила (ЭДС = напряжение).

В происходит от «напряжение», а E от «электродвижущая сила (ЭДС)».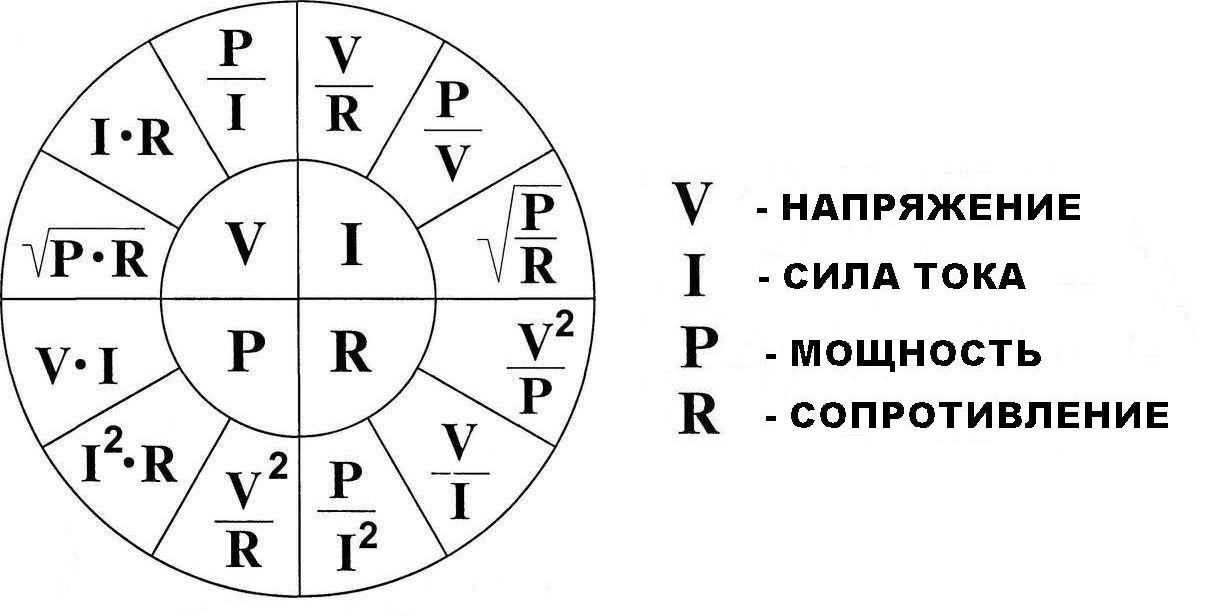 E означает также энергия , поэтому мы выбираем V . Энергия = напряжение × заряд. Е = В × Q . Некоторым лучше придерживаться E вместо V , так что делайте это. Для R взять Z .

См. также: Колесо формулы акустики (аудио)

Формула мощности 1 – Уравнение электрической мощности: Мощность P = I × В = R × I 2 2 2 90 90 6 ⁄ R  где мощность P в ваттах, напряжение В в вольтах, а ток I постоянного тока в амперах. Если есть переменный ток, посмотрите также на коэффициент мощности PF = cos φ и φ = угол коэффициента мощности (фазовый угол) между напряжением и силой тока.  Электричество Энергия равно E = P × т − измеряется в ватт-часах или также в кВтч. 1J = 1n × M = 1W × S Формула мощности 2 — Уравнение механической мощности: Power P = E ⁄ T , где Power 661 9 9 9 9 9 . Вт, Мощность P = работа/время ( Вт ⁄ t ). Энергия E в джоулях, а время t в секундах. 1 Вт = 1 Дж/с.  Мощность = сила, умноженная на смещение, деленная на время P = F × с/т или Мощность = сила, умноженная на скорость (скорость) P = F × v.   Неискаженного мощного звука в этих формулах не найти. Пожалуйста, берегите уши! Барабанная перепонка и диафрагма микрофона действительно двигаются только волнами . звуковое давление . Что не делает ни интенсивность, ни мощность, ни энергия. Если вы занимаетесь аудиозаписью, разумно не заботиться об энергии, мощность и интенсивность как причина , больше заботьтесь о эффекте звукового давления p и уровень звукового давления в ушах и в микрофонах и посмотрите на соответствующий аудио напряжение В ~ р ; см.: Звуковое давление и звуковая мощность − следствие и причина важно эффективность громкоговорителей. Сюда входит типичный вопрос: Сколько децибел (дБ) на самом деле в два или три раза больше громкости?  На самом деле среднеквадратичная мощность отсутствует. Слова «среднеквадратическая мощность» неверны. Есть расчет мощности, которая является произведением среднеквадратичного напряжения и среднеквадратичного тока. Вт RMS не имеет смысла. На самом деле, мы используем этот термин как крайнее сокращение мощности в . ватты рассчитаны по измерению среднеквадратичного значения напряжения. Пожалуйста, прочитайте здесь: Почему не существует таких понятий, как «среднеквадратичное значение ватт» или «ватт среднеквадратичное значение» и никогда не было.  Мощность «среднеквадратичная» — это довольно глупый термин, получивший распространение среди специалистов по аудиотехнике. Мощность – это количество энергии, которое преобразуется в единицу времени. Ожидайте платить больше, когда требуя большей мощности.

Андр-Мари Ампре был французским физиком и математиком. Его именем названа единица измерения электрического тока в системе СИ ампер . Алессандро Джузеппе Антонио Анастасио Вольта был итальянским физиком. В его честь была названа единица измерения электрического напряжения в системе СИ вольт . 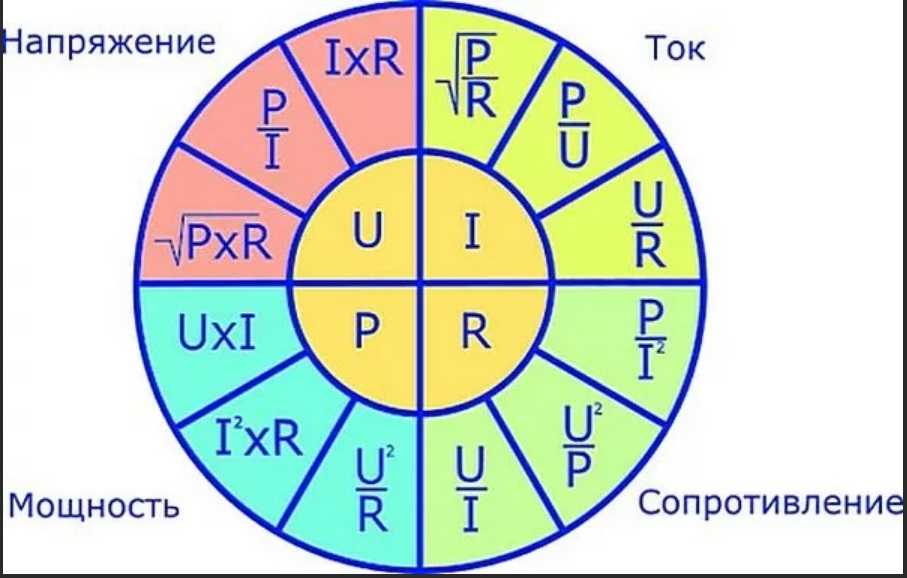Георг Симон Ом — немецкий физик и математик. Его именем названа единица измерения электрического сопротивления в системе СИ, равная Ом Ом. Джеймс Уатт был шотландским изобретателем и инженером-механиком. Его именем названа единица измерения электрической мощности (мощности) в системе СИ ватт .

Слово «усилитель мощности» используется неправильно, особенно в аудиотехнике. Напряжение и ток могут быть усилены. Странный термин «усилитель мощности» стал пониматься как усилитель, предназначенный для управления нагрузкой например громкоговоритель. Мы называем произведение усиления по току и усиления по напряжению «усилением мощности».

С помощью магического треугольника можно легко вычислить все формулы. Вы прячетесь с
пальцем вычисляемое значение. Два других значения показывают, как производить вычисления.
 

Расчеты: закон Ома — магический треугольник Ома
Измерение входного и выходного импеданса

ПЕРЕМЕННЫЙ ТОК (AC) ~

В _l = линейное напряжение (вольт), В _p = фазное напряжение (вольт), I _l = линейный ток (ампер), ампер)
Z = импеданс (Ом), P = мощность (ватт), φ = угол коэффициента мощности, VAR = вольт-ампер (реактивный)

Ток (одна фаза): I = P / В p × cos φ	Ток (3 фазы): I = P / √3 V L × COS φ или I = P /3 V 9065 P60606060606060606060606060606060606060606060606060606060. 0. 0. 6060660. 0. 0. 0. 0. 0. 0. 60660. 0. 0. 0. 0. 0. 0. 0.19660. 0. 0.
Мощность (одна фаза): P = В p × I p ×cos φ	Мощность (3 фазы): P = √3 В л × I l × cos φ или P = √3 V p × I p × φ 1 0 0 60 9060 60

Формулы мощности постоянного тока Напряжение В дюйм (В) расчет по току I дюйм (А) и сопротивлению R дюйм (Ом): В (В) = I (А) R (Ом) Мощность P в (Вт) расчет от напряжения V в (v) и ток I в (A): P (W) = В (V) × I (A) 666. . . . 1. . . 9. 9. (a) 6. (V) / R (Ω) = I 2 (A) R (Ω)   AC power formulas Напряжение В в вольтах (В) равно силе тока I в амперах (А), умноженной на импеданс Z в омах (Ом): В (В) = I (А) Z ((Ом) = (| 1 0 Z) | 0 | и ( θ I + θ Z ) Полная мощность S в вольт-амперах (ВА) равна напряжению В в вольтах (В), умноженному на ток I в амперах (А): S (ВА) = В (В) И (А) = (| В | × | I |) и ( θ В − θ I ) Реальная мощность P в ваттах (Вт) равна напряжению В в вольтах (В), умноженному на ток I в амперах (А), умноженному на коэффициент мощности (cos φ ): P (Вт) = В (В) × I (A) × 000 1 φ Реактивная мощность Ом в вольт-амперах реактивной (ВАР) равно напряжению В в вольтах (В) умноженному на ток I в амперах (А) умноженному на синус комплексного фазового угла мощности ( φ ): Q (ВАР) = В (В) × I (А) × sin φ Коэффициент мощности (FP) равен абсолютному значению косинуса комплексного фазового угла мощности ( φ ): ПФ = | cos φ |

Дж/с

Поток электрического заряда Q обозначается как электрический ток I.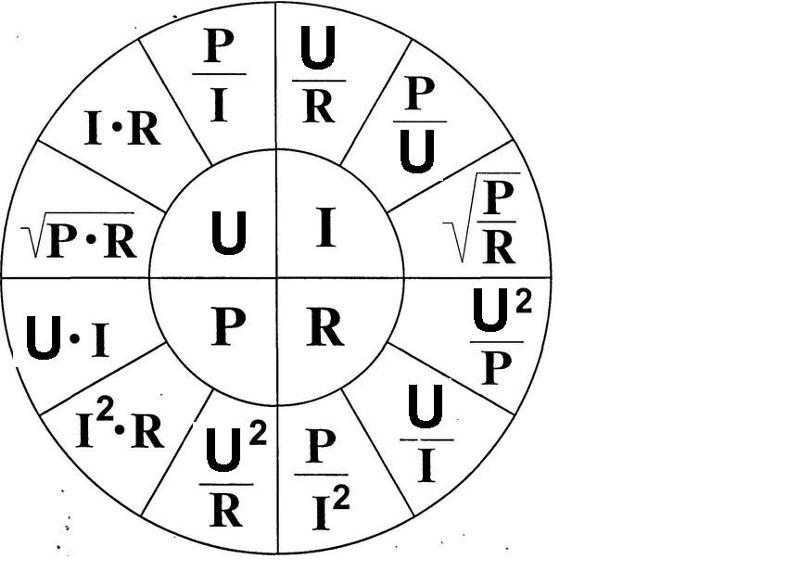 Количество заряда в единицу времени это изменение электрического тока. Ток течет с постоянной величиной I. за время t , он переносит заряд Q = I × t . Для постоянной во времени мощности соотношение между зарядом и током: I = Q/t или Q = I×t. Благодаря этому соотношению основные единицы ампер и секунда кулон в Установлена ​​международная система единиц. Кулоновскую единицу можно представить как 1 C = 1 A × s. Зарядка Q , (единица измерения в ампер-часах Ач), ток разряда I , (единица измерения в амперах А), время t , (единица измерения в часах ч).

В акустике у нас есть » Акустический эквивалент закона Ома »

Соотношения акустических величин, связанных с плоскими прогрессивными звуковыми волнами

Преобразование многих единиц, таких как мощность и энергия

префиксы |
длина |
площадь |
объем |
вес |
давление |
температура |
время |
энергия |
сила |
плотность |
скорость |
ускорение |
сила

[начало страницы]

Формула силы | Формула электроэнергии в цепях постоянного и переменного тока

Мы используем электроэнергию, предоставляемую нашей коммунальной компанией, для обеспечения нас светом, теплом, работающими приборами и т. д. Поскольку электрический потенциал (напряжение) и ток являются двумя величинами, доступными нам, когда коммунальная служба поставляет электрическую энергию, эти два параметра являются основными параметрами, определяющими электрическую мощность. В этом руководстве давайте подробно рассмотрим электрическую мощность, формулу электрической мощности в цепях переменного и постоянного тока.

Краткое описание

Что такое электроэнергия?

Электрическая энергия является одной из широко используемых форм энергии в нашей повседневной жизни, будь то питание от сети переменного тока или батареи. Наша коммунальная компания поставляет эту электрическую энергию в виде электрического потенциала и тока, а скорость, с которой электрическая энергия передается в электрической цепи, называется электрической мощностью.

С точки зрения физики, энергия — это способность выполнять работу, а скорость выполнения этой работы называется мощностью.

Итак, если P — мощность, W — работа, а t — время, то

мощность P = работа, выполненная в единицу времени = Вт/т

Единицами мощности являются ватты.

Мы знаем, что электрический потенциал — это количество работы, совершаемой при перемещении единичного заряда, а ток — это скорость движения заряда.

Используя приведенное выше утверждение, мы можем переписать предыдущее уравнение мощности как:

P = Вт/t = (Вт/Q) × (Q/t) Вт

Первый член (Вт/Q) представляет собой электрический потенциал (V), а второй член (Q/t) представляет ток (I).

Итак, электрическая мощность P = V × I.

Формула электрической мощности в цепях переменного и постоянного тока

В зависимости от типа тока в цепи, т. е. переменного тока или постоянного тока, электрическая мощность может быть дополнительно классифицирована на переменный ток. Мощность и мощность постоянного тока.

Давайте теперь посмотрим на различные формулы электроэнергии в цепях постоянного и переменного тока.

Формулы мощности в цепях постоянного тока

В простых цепях постоянного тока, т. е. электрических цепях с источником питания постоянного тока, формула мощности приведена ниже:

P = V × I

Мощность в резистивных цепях постоянного тока — это просто произведение напряжения и тока.

Мы можем вывести дополнительные формулы мощности, применяя закон Ома. Согласно закону Ома, напряжение в цепи (или компоненте) является произведением сопротивления и тока.

V = I × R

Итак, если мы используем это уравнение в приведенной выше формуле мощности, мы получим

P = V × (V/R) = V ² /R

P = (I×R ) × I = I ² R

В зависимости от имеющихся величин можно использовать одну из трех формул мощности для расчета мощности постоянного тока.

Формулы мощности в цепях переменного тока

Измерение мощности в цепях постоянного тока очень просто, так как все, что вам нужно сделать, это умножить напряжение и силу тока. Но то же самое невозможно в цепях переменного тока, поскольку значения напряжения и тока постоянно меняются как по величине, так и по направлению (знаку).

Значения переменного напряжения и тока обычно записываются как

В _{Переменный ток} = В _P × sin(ωt) и I _{Переменный ток} = I _P × sin(ωt)

Чтобы рассчитать мощность переменного тока, мы должны каким-то образом рассчитать средние значения напряжения и тока. Математически мы используем среднеквадратичное значение или среднеквадратичное значение для определения средних значений синусоидальных функций.

Если V _RMS является среднеквадратичным значением напряжения переменного тока, а I _RMS является среднеквадратичным значением переменного тока, то средняя мощность переменного тока равна

P _AC (среднее) = V _RMS × I _RMS

Если f(t) является функцией времени t, то ее среднеквадратичное значение равно

Применение вышеуказанной формулы к нашим чередующимся напряжению и тока синусоидальных значений, мы получаем:

V _ОБРАТА = V _P /√2 и I 9065 RMS _{= P} /√2 и I 9065 RMS _{= I rms = I . 2}

Мощность, которую мы рассчитали ранее (P _AC (Average)) на самом деле известна как полная мощность. Это не что иное, как произведение среднего (или эффективного) напряжения и тока, т. Е. Это максимальная средняя мощность, подаваемая на чисто резистивную нагрузку.

Но катушки индуктивности и конденсаторы имеют фазовые сдвиги и реактивное сопротивление. Итак, с катушками индуктивности и конденсаторами есть еще два способа определить мощность в цепях переменного тока. Это реальная мощность (активная мощность) и реактивная мощность.

Реальная мощность, также известная как активная мощность, представляет собой мощность, рассеиваемую в цепи из-за ее резистивных элементов.

Активная мощность = В _СКЗ × I _СКЗ × cos(θ), где θ — фазовый угол, на который напряжение опережает ток.

Реактивная мощность — это мощность, рассеиваемая в цепи за счет индуктивности и емкости (или реактивного сопротивления).

Задается как реактивная мощность = В _СКЗ × I _СКЗ × sin(θ)

Таким образом, мы можем сказать, что (полная мощность) ² = (активная мощность) ² + (реактивная мощность ) ²

Формулы мощности постоянного и переменного тока

В следующей таблице перечислены все формулы мощности для цепей переменного и постоянного тока.

Заключение

Простое руководство по пониманию электроэнергии.