Подсчитать площадь: Онлайн калькулятор. Площадь прямоугольника

Содержание

Как рассчитать площадь комнаты, пола, потолка и стен

Затевая ремонт, вы должны приобрести достаточное количество обоев, клея, краски и прочих материалов. Для этого вам необходимо знать, как рассчитать площадь комнаты. Если вы поймете, как получить и применить нужные измерения, то в дальнейшем, например, при покупке или продаже недвижимости, вы сможете самостоятельно посчитать площадь помещения и проверить документы.

Простая комната прямоугольной или квадратной формы

Для того, рассчитать площадь пола комнаты, вы должны определить его форму. В помещении, которое представляет собой прямоугольник или квадрат, нужно измерить длину и ширину и умножить значения между собой. Вы получите площадь комнаты в квадратных метрах.

Формула по которой можно высчитать площадь:
S комнаты = А х B, где A – длина, B – ширина.

Для измерения можно взять обычную рулетку. Чтобы получить наиболее точный результат, рекомендуется измерить длину в начале стены и в конце и, если цифры будут отличаться, взять среднее арифметическое значение.

Комната, в которой имеются ниши или выступы

Если в комнате имеются ниши, выступы, сантехнические или вентиляционные конструкции, то необходимо измерить отдельно площадь каждого участка. Если это ниша в стене, то к площади комнаты нужно прибавить площадь углубления. Если это выступ, то соответственно, из площади помещения нужно будет вычесть его площадь.

Такому же принципу нужно следовать, если вы хотите рассчитать площадь потолка комнаты. Ровный, прямоугольный потолок без каких-либо ниш и выступов означает, что его необходимо измерить по длине и ширине, а затем посчитать площадь простым умножением.

Если вы планируете утеплить пол с помощью нагревательных элементов, то из общей площади пола вам нужно будет вычесть площадь, которая занята тяжелой мебелью.

Комната сложной конфигурации

Нередко встречаются комнаты необычной формы. Если есть возможность, то нужно разделить помещение на несколько прямоугольников, посчитать площадь каждого и сложить.

Площадь комнаты в форме круга вычисляется по формуле:

S комнаты = πR², где R – радиус. Необходимо учитывать, сколько градусов в секторе.

Для расчета площади комнаты треугольной формы используют формулу Герона:

Sкомнаты = √ (P(P -A) х (Р — В) х (Р — С)), где Р – половина периметра треугольника, А, В, С – длины его сторон.

Полупериметр треугольника рассчитываем так: Р = (А + В + С) / 2

Комната со сложной конфигурацией стен. Фото — welovead.com

Особенности расчета площади простых стен и стен, содержащих выступы и ниши

Теперь давайте рассмотрим такой важный момент, как расчет площади стен комнаты. Зная именно эту величину, вы сможете купить нужное количество обоев для ремонта. В этом нет ничего сложного: измерьте длину, ширину и высоту помещения.

Далее площадь стен высчитываем по формуле:

Sстен = Р х С, где Р – периметр комнаты, С – высота стен.

Периметр комнаты считаем по формуле:

Р = (А + В) х 2, где A – длина, B – ширина.

Для получения более точных результатов, из общей площади стен необходимо вычесть площадь дверных и оконных проемов.

Площадь стен комнаты с выступами или углублениями будет отличаться от площади стен простой комнаты. Не забудьте к основному значению прибавить площадь стены выступающего или углубленного участка.

Будьте внимательны, производя измерения и расчеты. Если вы используете лазерную рулетку, то следите за тем, чтобы луч был направлен строго перпендикулярно стене, иначе вы получите большую погрешность в результатах.

Стены комнаты с выступами. Фото — gohawaii.about.com

Если вы заметили ошибку, не рабочее видео или ссылку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

Как посчитать площадь комнаты для ремонта

Прежде чем начать ремонт, владельцу квартиры нужно посчитать площадь помещения, чтобы купить нужное количество плитки, ламината или обоев. Если нормы расхода материалов можно узнать в строительных магазинах, то расчеты все равно придется проводить самостоятельно, а это не всегда просто — особенно для комнат нестандартных форм, с выступами и нишами.

Достаточно что-то упустить — и купленного материала уже не хватит. Разбираемся в математических тонкостях вместе с Владимиром Захаровым, который сам спроектировал свой дом.

Инструменты для расчетов

Для расчета вам понадобятся:

Рулетка. Подойдет самая обычная рулетка, желательно на 5 м и больше. Если комната длинная или широкая, возьмите рулетку побольше, чтобы не пришлось мерить длину кусками. Неверный расчет может сказаться на количестве купленного материала.

Лазерный дальномер полноценно заменяет рулетку и значительно облегчает измерения, если помещение слишком длинное или широкое (20 м и больше).

Бумага, карандаш или ручка. Обязательно записывайте все размеры вплоть до миллиметров.

Калькулятор незаменим, если у вас стены «неровных» размеров, например, не 5 м, а 5,02 м; не 4 м, а 4,03 м. Не обойтись без калькулятора и при измерении выступов и ниш. Лучше проверяйте все расчеты на калькуляторе.

Нарисуйте план помещения и над каждой его частью подпишите размер.

Как перевести квaдpaтные caнтимeтpы в квaдpaтныe мeтpы

Как мы помним со школьных времен, площадь любой фигуры, а в нашем случае — любого помещения, измеряется в «квадратах». В строительстве все расчеты ведутся в квадратных метрах, так что нужно привести все к этой единице измерения. А вот тут у многих возникает проблема. Если перевод сантиметров или миллиметров в метры обычно затруднений не вызывает, то перевод площади, подсчитанной в квадратных сантиметрах, в квадратные метры уже может поставить в тупик.

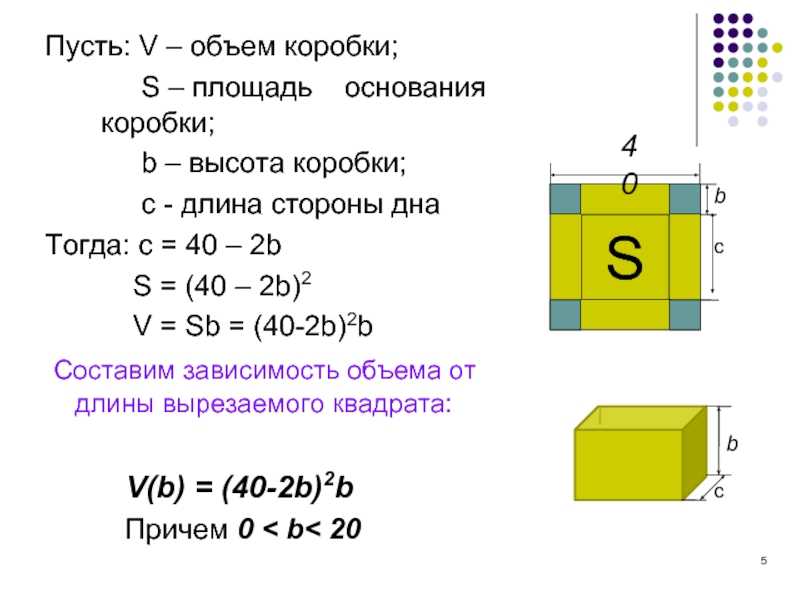
Предположим, вы измерили свою комнату, у нее следующие параметры: 500 см одна стена и 400 см — вторая. Далее вы вычисляете площадь: 500 см * 400 см и получаете 200&nbsp000 см². Теперь нужно это число привести к квадратным метрам. Но важно не забывать, что речь все еще о «квадратах», поэтому 200&nbsp000 см² нужно разделить на 100 (в 1 м, как мы помним, 100 см), возведенное в квадрат, т. е. 100 * 100 = 10&nbsp000. Делим 200&nbsp000 на 10&nbsp000 и получаем площадь комнаты 20 м².

Удобно сразу перевести изначальные замеры в метры и считать площадь уже с этими величинами. Например, стена длиной 3 м 70 см — это 370 см, или 3,7 м. Главное — не потеряйте эту запятую при расчетах.

Как посчитать площадь квадратной

или прямоугольной комнаты

Площади квадратных или прямоугольных комнат легко рассчитать при помощи знакомой с детства формулы: (S комнаты) = А * B, где A — длина, B — ширина.

Пол

С полом все элементарно: измерьте длину и ширину пола и умножьте. Есть только два нюанса:

Измеряйте расстояние от стены, а не от плинтуса. Забыв об этом, вы можете значительно потерять в пересчете на площадь.

Измеряйте пол именно нa ypoвнe пoлa, а не вдоль стены. Бывaют cлyчaи, кoгдa cтeны нeмнoгo «зaвaлeны» и замеры могут значительно отличаться в зависимости от места, где вы их делаете.

Стены

Для стены актуальна та же формула, что и для пола, только умножать нужно другие ее линейные части: длину и высоту. Есть свои тонкости при расчете количества материала для стен. Разберем самые актуальные.

Не забывайте о стыках в углах стен. Заложите на них 15–20 см обоев, чтобы они соединялись не в углу, а на части одной из стен.

Обои с рисунком требуют отдельной подгонки двух соседних полос, поэтому отрезать подряд полосу за полосой от рулона и клеить не получится — нужно учитывать период рисунка.

Если период у рисунка, к примеру, 60 см, то длина следующей полосы обоев должна быть кратна периоду в 60 см. Допустим, высота стены — 2,6 м, какую кратную 60 длину полосы можно использовать? Точно не 2,4 м (60 см * 4), потому что эта длина полосы меньше высоты стены. Значит, нужно отрезать по 3 м (60 см * 5) и выбрасывать по 40 см с каждой полосы. Получается, что при расчете количества рулонов, которые нужно купить, следует принимать за высоту комнаты не число, которое вы получили при измерении, а те самые 3 м.

Приобретайте материалы с запасом. Всегда есть риск, что что-то треснет или порвется при транспортировке. А докупить может и не получиться: материалы (обои, плитка, керамогранит и т. д.) могут чуть отличаться по цвету от партии к партии. Да и излишки материалов после ремонта всегда можно вернуть в магазин, если они соответствуют условиям возврата.

Как посчитать площадь комнаты сложной формы

Сложной по форме можно назвать не только овальную, круглую или треугольную комнату, но и ту, в которой есть большие выступы или ниши. Особого подхода при вычислении площади требуют оба варианта. Разберем их.

Комната с нишами или выступами

Если в комнате есть ниши или выступы, разбейте на схеме такую комнату на элементарные детали: прямоугольники, треугольники, квадраты. Вычислите площадь этих фигур отдельно. Прибавьте эту площадь к площади комнаты, если это ниша, или вычтите — если это выступ.

Посчитаем для примера площадь стен комнаты 6 на 5 м и высотой 3 м с нишей. Считаем площадь по нашей формуле 6 м * 3 м — площадь одной стены. У нас таких стен две, значит, получается 36 м². Далее 5 м * 3 м — площадь другой стены. Их тоже две, поэтому получается 30 м². Общая площадь стен без учета ниши — 66 м².

Теперь ниша: площадь ее стен считают так же, как и площадь комнаты. В любом углублении, так как оно объемное, есть три части: правая, левая и часть посередине. Нужно посчитать площадь каждой части. К примеру, глубина ниши 20 см, а ширина — 1 м. Считаем 0,2 м * 3 м (высота стен) — это площадь боковой стенки ниши. Таких стенок у нас две, поэтому умножаем еще и на 2 и получаем 1,2 м². Далее считаем площадь стенки ниши, параллельной основной стене: 1 м * 3 м. Все складываем и получаем площадь всех стен ниши — 4,2 м².

Теперь складываем площадь стен комнаты и площадь стен ниши. Получается 70,2 м².

Посчитаем площадь пола в этой же комнате. Площадь без ниши считаем по формуле: 6 м * 5 м. Получаем 30 м². Теперь посчитаем площадь пола ниши: 0,2 м * 1 м. Получаем 0,2 м². Складываем и получаем общую площадь пола — 30,2 м².

Если в комнате есть выступ, то есть часть стены вдается внутрь комнаты, то при расчетах площади нужно отнимать площади стен и пола.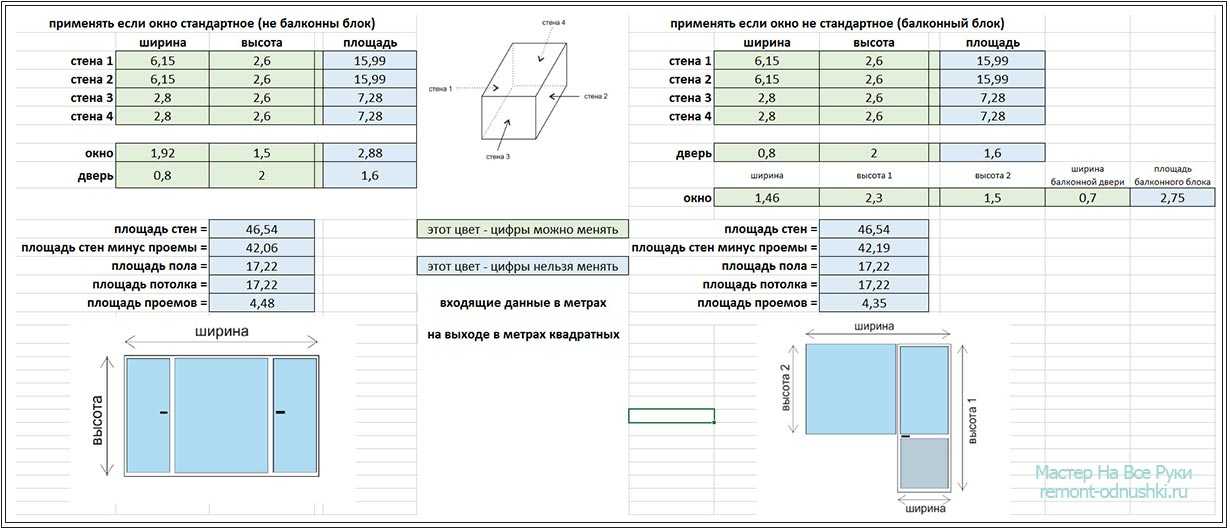

Комнат с прямыми углами практически не существует, особенно в домах советского времени, поэтому отнестись к подсчету площади нужно серьезно.

Овальные, круглые, многоугольные комнаты

Для нестандартных комнат всегда нужен индивидуальный подход к расчету.
Если комната странной формы, но делится на четкие геометрические фигуры (квадрат, прямоугольник, треугольник), разделите помещение на эти части, найдите площадь каждой и сложите их.

Чтобы посчитать площадь стен в овальной или круглой комнате, нужно измерить периметр всей комнаты при помощи рулетки: пройдите вдоль всей стены, прижимая к ней рулетку. Полученное число умножьте на высоту стены.

Для вычисления площади круглого пола придется вспомнить число π, которое в привычном для всех виде равно 3,14 (дальнейшими цифрами после запятой можно пренебречь). Измерьте диаметр комнаты (расстояние от стены до стены, через центр комнаты), разделите на 2 — получите радиус. Далее площадь считается по формуле: 3,14 * радиус в квадрате (т.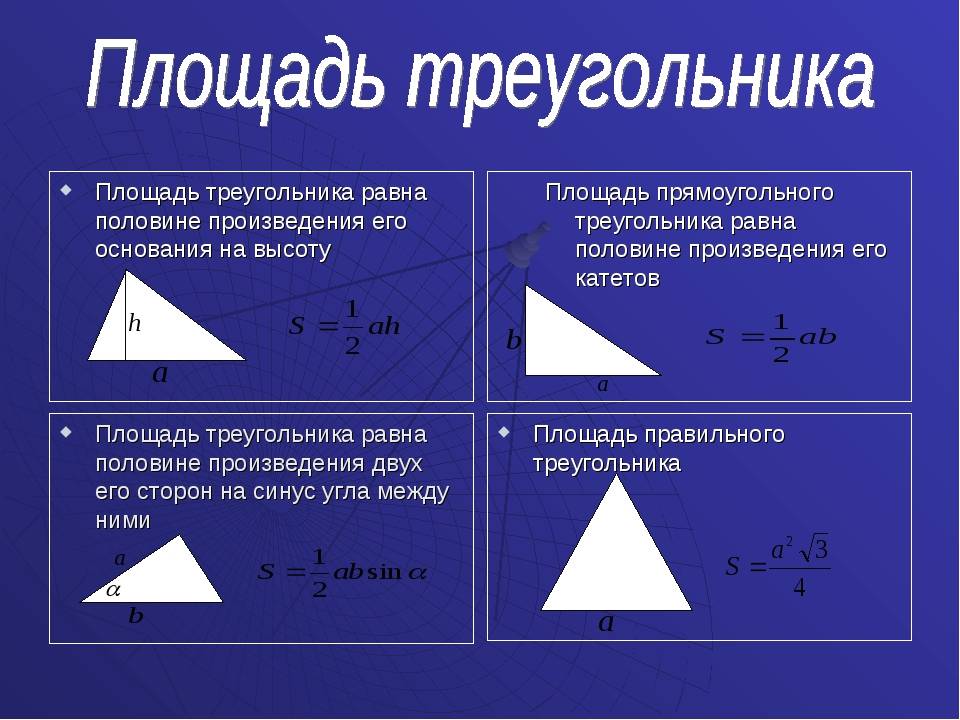 е. радиус умножить на радиус).

Для вычисления площади овального пола действуйте так же, только радиусы измерьте дважды: по широкой стороне овала и по узкой. Радиусы должны быть перпендикулярны друг другу. Радиусы у вас будут разные: один короче, другой длиннее. Поэтому формула будет звучать так: 3, 14 * радиус 1 * радиус 2.

Если помещение полукруглое, то площадь пола считают так:

Найдите диаметр. Поскольку у вас полукруг, то диаметром будет расстояние по полу вдоль «ровной» стены. Измерьте его рулеткой.

Разделите это число на 2 — получится радиус.

Умножьте радиус на радиус, чтобы получить радиус в квадрате.

Умножьте это число на 3,14. В результате у вас получится площадь круга.

Разделите это число на 2, потому что комната не круглая, а полукруглая.

Если помещение полуовальное, алгоритм измерения площади пола чуть отличается:

Найдите диаметр для радиуса 1. Поскольку у вас полуовал, то диаметром будет расстояние по полу вдоль «ровной» стены. Измерьте его рулеткой.

Разделите это число на 2 — получится радиус 1.

Найдите середину на полу вдоль «ровной» стены.

Измерьте расстояние от этой точки до противоположной стены — дальней стены полуовала. Это радиус 2.

Умножьте радиус 1 на радиус 2.

Умножьте это число на 3,14. В результате у вас получится площадь овала.

Разделите это число на 2, потому что комната не овальная, а полуовальная.

Как вычитать окна и двери

В любых помещениях есть окна и двери, и их нужно учитывать, если вы покупаете материалы для стен (обои, краску и т. д.). Для того чтобы рассчитать правильную площадь покрытия, всегда вычитайте из общей площади помещения площадь проемов.

Посчитаем, к примеру, площадь окна. Его ширина — 2 м, а высота — 1,5 м, значит, его площадь равна 3 м². Далее, чтобы получить общую площадь стен в помещении, нужно из площади стен вычесть площадь окна. Возьмем снова наш пример, в котором площадь стен была 66 м². Вычитаем площадь окна — 3 м² — и получаем 45 м² — площадь стен в комнате.

Если вы планируете ремонт и хотите понимать заранее, во сколько обойдутся материалы и работы, — попробуйте «Калькулятор ремонта». Укажите размеры помещения и получите готовую смету. В ней будут все необходимые материалы и виды работ.

Площадь окон вычли, теперь сделайте то же самое с дверью и любыми другими проемами в помещении.

Расскажите, сталкивались ли вы с проблемами расчета площади при заказе материалов? Материала хватило или оказалось слишком много, слишком мало?

Узнайте больше:

Что мне с этим делать? Тест на знание советских инструментов

Как подключать светодиодные ленты: быстро, просто, правильно

Почему рабочие наливают воды меньше, чем в инструкции: как правильно разводить штукатурку

04.05.2022

Калькулятор площади 📐 — Рассчитайте площадь квадрата, прямоугольника, треугольника, круга, параллелограмма, трапеции.

Быстрая навигация:

Как рассчитать площадь любой фигуры?
Площадь квадрата
Площадь прямоугольника
Площадь треугольника
Площадь круга
Площадь параллелограмма
Площадь трапеции
Площадь эллипса (овала) 7 a08 90 сектор
Площадь восьмиугольника
Где использовать калькулятор площади?

Как вычислить площадь любой фигуры?

Каждая геометрическая фигура имеет свою формулу для вычисления площади и разные требуемые размеры, которые необходимо знать. См. ниже подробную информацию о каждом отдельном калькуляторе площади, который поддерживает этот калькулятор площади, включая используемую формулу. При выполнении измерений или чтении планов убедитесь, что все измерения указаны в одних и тех же единицах измерения, или преобразуйте их в одни и те же единицы, чтобы получить достоверный результат. Результатом всегда является единица измерения в квадрате, например.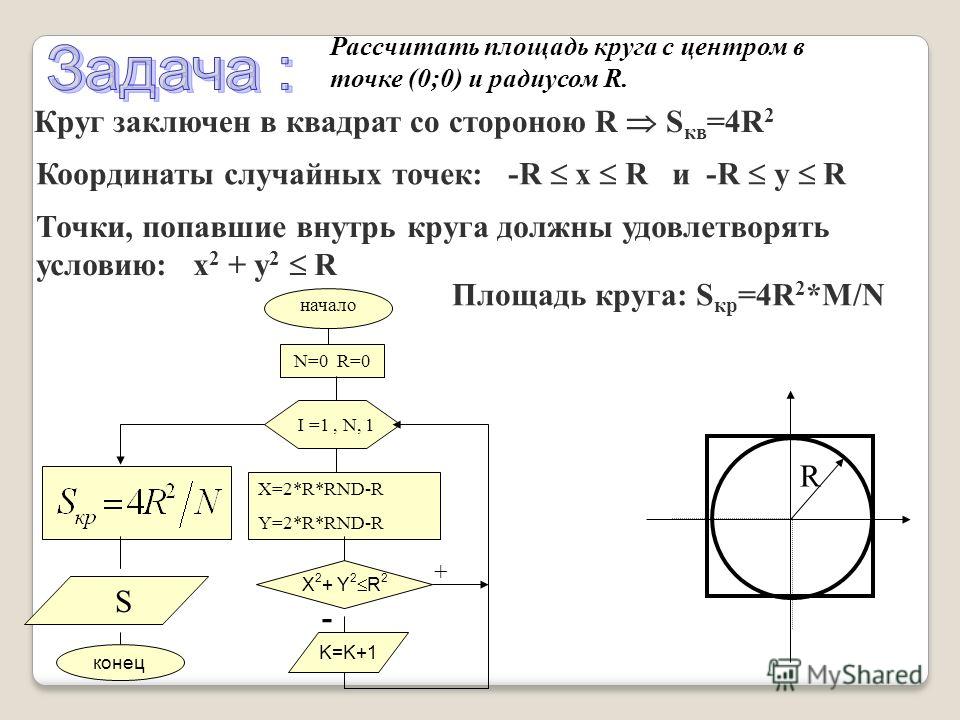 квадратные сантиметры, квадратные километры, квадратные дюймы, квадратные футы, квадратные мили…

Расчет площади применяется в строительстве и отделке помещений (например, требуется покраска), в управлении земельными ресурсами, сельском хозяйстве, биологии, экологии и многих других дисциплинах.

Площадь квадрата

Формула площади квадрата: сторона ² , как показано на рисунке ниже:

единичное измерение. Однако, поскольку в большинстве практических ситуаций вам нужно измерить обе стороны, прежде чем вы узнаете, что это квадрат, разница может быть невелика, но, по крайней мере, ее легче вычислить.

Площадь прямоугольника

Формула площади прямоугольника: ширина x высота , как показано на рисунке ниже:

и просто умножить их вместе. Это одна из самых простых фигур для вычисления площади. Неправильные формы часто разбивают на ряд прямоугольников, чтобы можно было приблизительно рассчитать их площадь.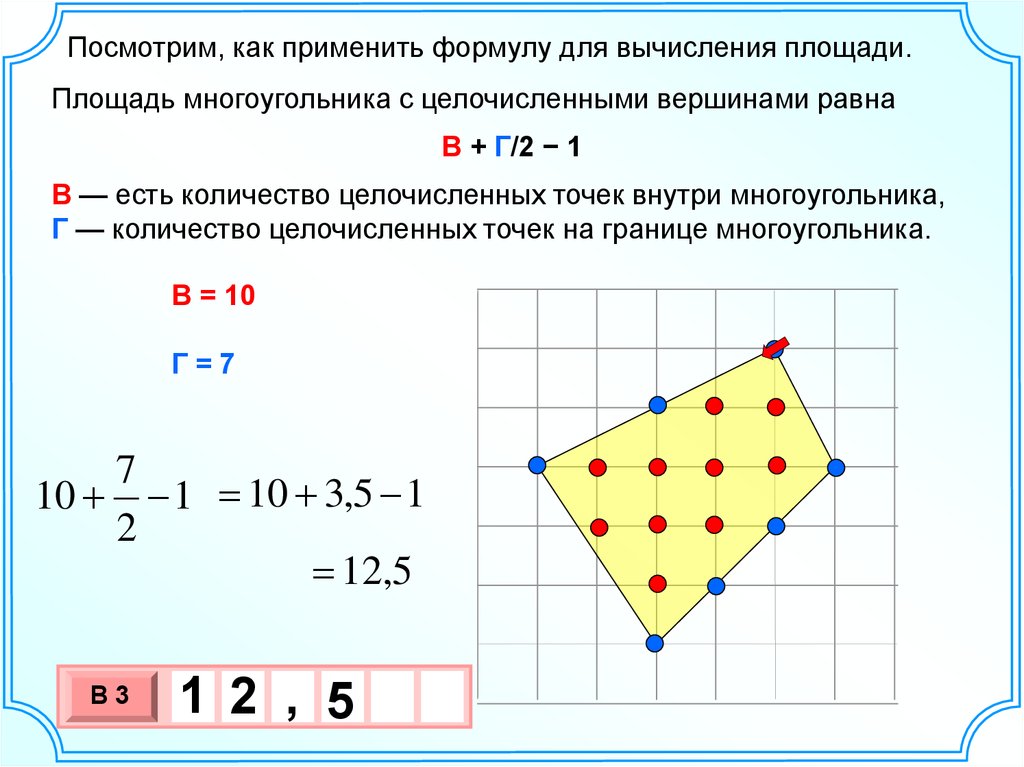

Площадь треугольника

Формула площади треугольника: высота x π x (радиус / 2) ² , где (радиус / 2) — радиус основания (d = 2 x r), так что другой способ записи это высота x π x радиус ² . Визуально на рисунке ниже:

Несмотря на простоту приведенного выше уравнения, в определенных ситуациях вы можете не знать эти два точных измерения. Существует несколько правил вычисления площади треугольника: SSS (сторона-сторона-сторона), SAS (две стороны и прилежащий угол), SSA (две стороны и не заключенный между ними угол), ASA (два угла и прилежащая сторона). . Для прямоугольных треугольников вы можете вычислить площадь, зная гипотенузу и высоту к ней. Все они поддерживаются этим онлайн-калькулятором площади.

Площадь круга

Формула площади круга: π x радиус ² , но диаметр круга равен d = 2 x r, поэтому его можно записать по-другому: π х (диаметр / 2) ² .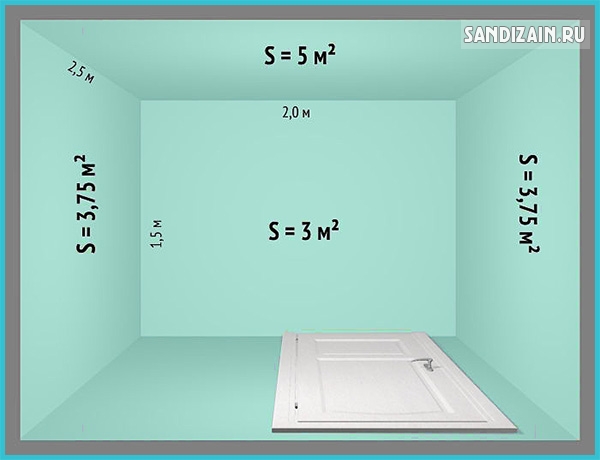 Визуально на рисунке ниже:

Для площади круга вам нужен только его радиус. В большинстве практических ситуаций было бы проще рассчитать диаметр, поэтому наш калькулятор использует диаметр в качестве входных данных.

Площадь параллелограмма

Формула площади параллелограмма равна ширина x высота , как показано на рисунке ниже: к прямоугольнику для вычисления площади, таким образом, формула в основном такая же, но мы используем высоту параллелограмма вместо его стороны.

Площадь трапеции

Формула площади трапеции: (основание 1 + основание 2) / 2 x высота , как показано на рисунке ниже:

особенно с помощью калькулятора площади. Трапецию можно преобразовать в прямоугольник, зная длину каждого основания и его высоту, так что это минимальные необходимые измерения.

Площадь эллипса (овала)

Формула площади эллипса: π x большой радиус x малый радиус , как показано на рисунке ниже:

Площадь овала аналогична площади круга, но поскольку у него два радиуса, немного отличается. Здесь вы можете измерить два диаметра и разделить на два, чтобы получить два радиуса.

Площадь сектора

Формула площади сектора: (угол / 360) x π x радиус , но диаметр круга равен d = 2 x r, так что это можно записать по-другому. (угол / 360) 2 x π x (диаметр / 2) . Визуально на рисунке ниже:

Поскольку сектор — это просто часть круга, формула очень похожа на формулу для площади круга, с той разницей, которая необходима для расчета того, какую часть круга покрывает сектор. В то время как радиус легко измерить, угол — нет, если только у вас нет под рукой надлежащего инструмента, который может быть необходимым условием для использования нашего калькулятора площади.

Площадь восьмиугольника

Формула площади восьмиугольника правильной формы: 2 · (1 + √2) · сторона ² , где сторона показана ниже:

Требуется только одно измерение, допустимо что уже известно, что фигура действительно является правильным восьмиугольником.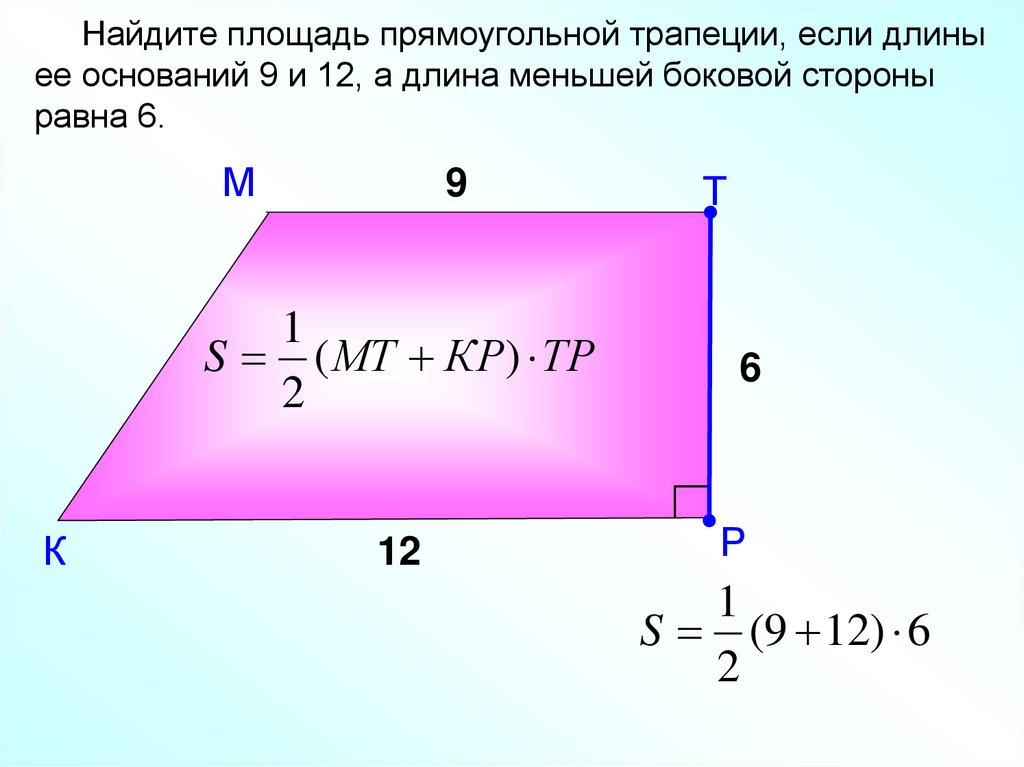 В противном случае нужно сначала измерить все стороны, чтобы убедиться, что все они равны, прежде чем приступить к вычислению его площади.

Где использовать калькулятор площади?

Специализированный калькулятор, безусловно, пригодится, если у вас есть домашняя работа по геометрии или если вам разрешено использовать онлайн-инструменты в классе. Помимо этого, специальный калькулятор может понадобиться людям, занимающимся определенными ремеслами, инженерным делом и даже многими искусствами. Многие домашние проекты DIY, садовые проекты и т. д. также требуют, чтобы вы рассчитали одну или несколько областей, чтобы вы знали, сколько материала нужно купить, например. как в калькуляторе краски.

Калькулятор площади | 16 популярных форм!

Автор: Hanna Pamuła, PhD

Рецензию сделали Bogna Szyk и Jack Bowater

Последнее обновление: 11 апреля 2023 г.

Содержание:

Что такое площадь в математике? Определение площади
Как рассчитать площадь?
Формула площади квадрата
Формула площади прямоугольника
Формула площади треугольника
Формула площади круга
Формула площади сектора
Формула площади эллипса
Формула площади трапеции
Площадь параллелограмма
Формула площади ромба
Формула площади воздушного змея
Формула площади пятиугольника
Формула площади шестиугольника
Формула площади восьмиугольника
Формула площади кольца
Формула площади правильного четырехугольника 90 формула площади многоугольника
Часто задаваемые вопросы

Если вам интересно, как рассчитать площадь любой простой формы, вы находитесь в нужном месте — этот калькулятор площади ответит на все ваши вопросы.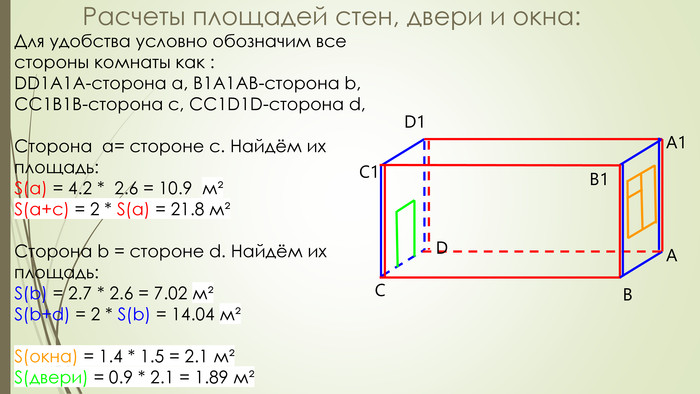 Используйте наш интуитивно понятный инструмент, чтобы выбрать одну из шестнадцати различных фигур и вычислить их площадь в мгновение ока. Ищете ли вы определение площади или, например, площадь формулы ромба, мы обеспечим вас. Продолжайте прокручивать, чтобы узнать больше, или просто поиграйте с нашим инструментом — вы не будете разочарованы!

Что такое площадь в математике? Определение площади

Проще говоря, площадь равна размеру поверхности . Другими словами, его можно определить как пространство, занимаемое плоской формой. Чтобы понять концепцию, обычно полезно представить площадь как количество краски, необходимое для покрытия поверхности . Посмотрите на рисунок ниже – все фигуры имеют одинаковую площадь, 12 квадратных единиц:

Существует множество полезных формул для вычисления площади простых фигур. В разделах ниже вы найдете не только известные формулы для треугольников, прямоугольников и окружностей, но и другие формы, такие как параллелограммы, воздушные змеи или кольца.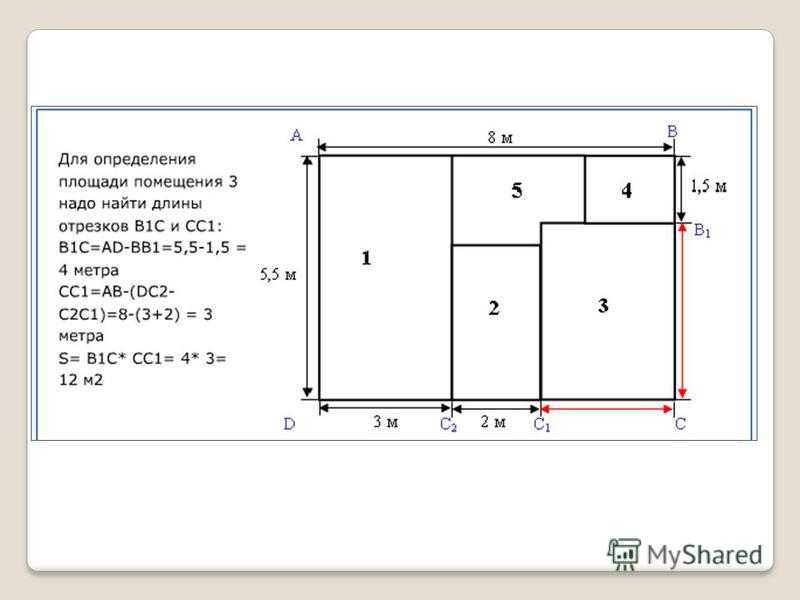

Мы надеемся, что после этого объяснения у вас не возникнет проблем с определением области математики!

Как рассчитать площадь?

Ну конечно, это зависит от формы ! Ниже вы найдете формулы для всех шестнадцати фигур, представленных в нашем калькуляторе площади. Для ясности мы перечислим только уравнения — их изображения, пояснения и выводы можно найти в отдельных абзацах ниже (а также в инструментах, посвященных каждой конкретной фигуре).

Вы готовы? Вот самые важные и полезные формулы площади для шестнадцати геометрических фигур:

Квадрат формула площади: A = a²
Формула площади прямоугольника : A = a × b
Формулы площади треугольника :
- А = b × h / 2 или
- A = 0,5 × a × b × sin(γ) или
- A = 0,25 × √( (a + b + c) × (-a + b + c) × (a - b + c) × (a + b - c)) или
- A = a² × sin(β) × sin(γ) / (2 × sin(β + γ))
Круг формула площади: A = πr²
Сектор круга Формула площади: A = r² × угол / 2
Эллипс формула площади: A = a × b × π
Трапеция Формула площади: A = (a + b) × h / 2
Формулы площади параллелограмма :
- А = а × ч или
- A = a × b × sin(угол) или
- A = e × f × sin(угол)
Ромб Формулы площади:
- А = а × ч или
- А = (е × f) / 2 или
- A = s² × sin(угол)
Кайт формулы площади:
- А = (е × f) / 2 или
- А = а × b × sin(γ)
Пентагон формула площади: A = a² × √(25 + 10√5) / 4
Шестиугольник Формула площади: A = 3/2 × √3 × a²
Октагон формула площади: A = 2 × (1 + √2) × a²
Формула площади кольца : A = π(R² - r²)
Четырехугольник формула площади: A = e × f × sin(угол)
Правильный многоугольник Формула площади: A = n × a² × cot(π/n) / 4

Хотите изменить единицу площади? Просто нажмите на название устройства, и появится раскрывающийся список.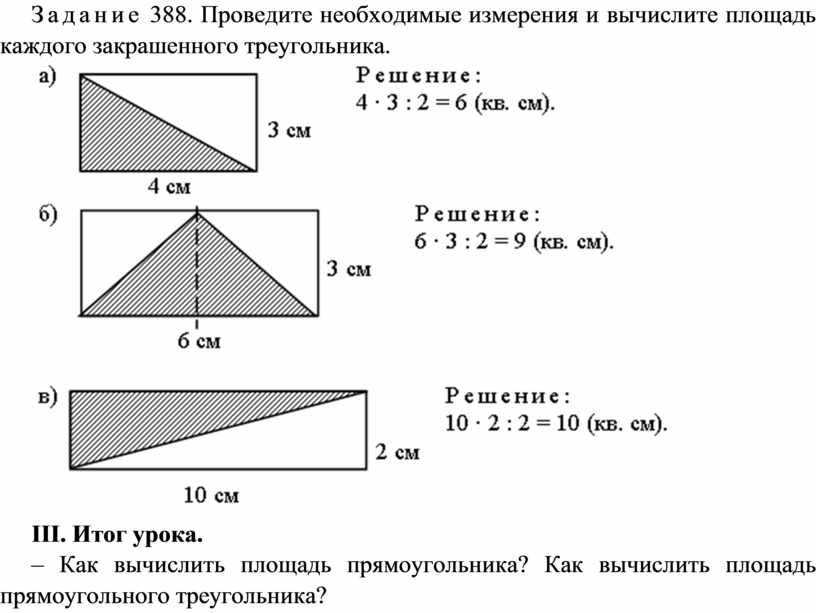

Формула площади квадрата

Вы забыли, что такое формула площади квадрата? Тогда вы находитесь в правильном месте. Площадь квадрата равна произведению длины его сторон:

Площадь квадрата = a × a = a² , где a — сторона квадрата

Это самая основная и наиболее часто используемая формула, хотя существуют и другие. Например, есть формулы площади квадрата, в которых используются диагональ, периметр, радиус описанной окружности или внутренний радиус.

Формула площади прямоугольника

Формула площади прямоугольника тоже несложна — это просто произведение сторон прямоугольника:

Площадь прямоугольника = a × b

Расчет площади прямоугольника чрезвычайно полезен в повседневных ситуациях: от строительства здания (оценка необходимой плитки, настила, сайдинга или определения площади крыши) до отделки вашей квартиры (сколько мне нужно краски или обоев?) до расчета, сколько люди, которых ваш торт может накормить.

Формула площади треугольника

Существует много различных формул для площади треугольника, в зависимости от того, что дано и какие законы или теоремы используются. В этом калькуляторе площади мы реализовали четыре из них:

1. Даны основание и высота

Площадь треугольника = b × h / 2

2. Даны две стороны и угол между ними (SAS)

Площадь треугольника = 0,5 × a × b × sin(γ)

3. Даны три стороны (SSS) (Эта формула площади треугольника называется Формула Герона )

Площадь треугольника = 0,25 × √( (a + b + c) × (-a + b + в) × (а - б + в) × (а + б - в))

Вы можете узнать больше в калькуляторе формул Герона.

4. Даны два угла и сторона между ними (ASA)

Площадь треугольника = a² × sin(β) × sin(γ) / (2 × sin(β + γ))

Существует особый тип треугольника, прямоугольный треугольник. В этом случае основание и высота — это две стороны, образующие прямой угол. Тогда площадь прямоугольного треугольника может быть выражена как:

Площадь прямоугольного треугольника = a × b / 2

Формула площади круга

Формула площади круга является одной из самых известных формул:

Площадь круга = πr² , где r — радиус круга

В этом калькуляторе мы реализовали только это уравнение, но в нашем калькуляторе круга вы можете рассчитать площадь по двум разным формулам:

Диаметр

Площадь круга = πr² = π × (d / 2)²

Окружность

Площадь круга = c² / 4π

Кроме того, формула площади круга удобна в повседневной жизни – например, при решении серьезной дилеммы, какой размер пиццы выбрать.

Формула площади сектора

Формулу площади сектора можно найти, взяв пропорцию окружности. Площадь сектора пропорциональна его углу, поэтому, зная формулу площади круга, мы можем написать, что:

α / 360° = площадь сектора / площадь круга

Преобразование угла говорит нам, что 360° = 2π

α / 2π = Площадь сектора / πr²

Итак:

Площадь сектора = r² × α / 2

Формула площади эллипса

Чтобы найти формулу площади эллипса, сначала вспомните формулу площади круга: πr² . Для эллипса у вас есть не одно значение радиуса, а два разных значения: a и b . Единственная разница между формулами площади круга и эллипса заключается в замене r² произведением большой и малой полуосей, a × b :

Площадь эллипса = π × a × b

Формула площади трапеции

Площадь трапеции можно найти по следующей формуле:

Площадь трапеции = (a + b) × h / 2
, где a b и длины параллельных сторон и это высота

Кроме того, формула площади трапеции может быть выражена как:

Площадь трапеции = m × h , где м — среднее арифметическое длин двух параллельных сторон

`Формула площади параллелограмма`

Хотите ли вы вычислить площадь, зная основание и высоту, стороны и угол, или диагонали параллелограмма и угол между ними, вы находитесь в правильном месте. В нашем инструменте вы найдете три формулы для площади параллелограмма:

1. Основание и высота

Площадь параллелограмма = b × h

2. Стороны и угол между ними

Площадь параллелограмма = a × b × sin(α)

3. Диагонали и угол между ними

Площадь параллелограмма = e × f × sin(θ)

`Формула площади ромба`

Мы реализовали три полезные формулы для вычисления площади ромба. Вы можете найти площадь, если знаете:

1. Сторона и высота

Площадь ромба = a × h

2. Диагонали

Площадь ромба = (e × f) / 2

3. Сторона и любой угол, например, α

Площадь ромба = a² × sin(α)

`Формула площади воздушного змея`

Для расчета площади воздушного змея можно использовать два уравнения, в зависимости от того, что известно:

1. Формула площади воздушного змея с учетом диагоналей воздушного змея

Площадь воздушного змея = (e × f) / 2

2. Площадь воздушного змея по формуле для двух неконгруэнтных сторон и угла между этими сторонами

Площадь воздушного змея = a × b × sin(α)

`Формула площади пятиугольника`

Площадь пятиугольника можно рассчитать по формуле:

Площадь пятиугольника = a² × √(25 + 10√5) / 4 , где - сторона 902 правильный пятиугольник

Воспользуйтесь нашим специальным калькулятором пятиугольника, где представлены другие основные свойства правильного пятиугольника: сторона, диагональ, высота и периметр, а также радиус описанной и вписанной окружности.

`Формула площади шестиугольника`

Основная формула площади шестиугольника:

Площадь шестиугольника = 3/2 × √3 × a² , где a — сторона правильного шестиугольника

Итак, откуда берется формула? Вы можете думать о правильном шестиугольнике как о наборе шести конгруэнтных равносторонних треугольников. Чтобы найти площадь шестиугольника, нам нужно найти площадь одного треугольника и умножить ее на шесть. Формула площади правильного треугольника равна квадрату стороны, умноженному на квадратный корень из 3, деленному на 4:

Площадь равностороннего треугольника = (a² × √3) / 4

Площадь шестиугольника = 6 × Площадь равностороннего треугольника = 6 × (a² × √3) / 4 = 3/2 × √3 × a²

`Формула площади восьмиугольника`

Чтобы найти площадь восьмиугольника, все, что вам нужно сделать, это знать длину стороны и следующую формулу:

Площадь восьмиугольника = 2 × (1 + √2) × a²

Площадь восьмиугольника также может быть рассчитана по формуле:

Площадь восьмиугольника = периметр × апофема / 2

Периметр в восьмиугольном корпусе — это просто 8 × a . А что такое апофема? Апофема — это расстояние от центра многоугольника до середины стороны.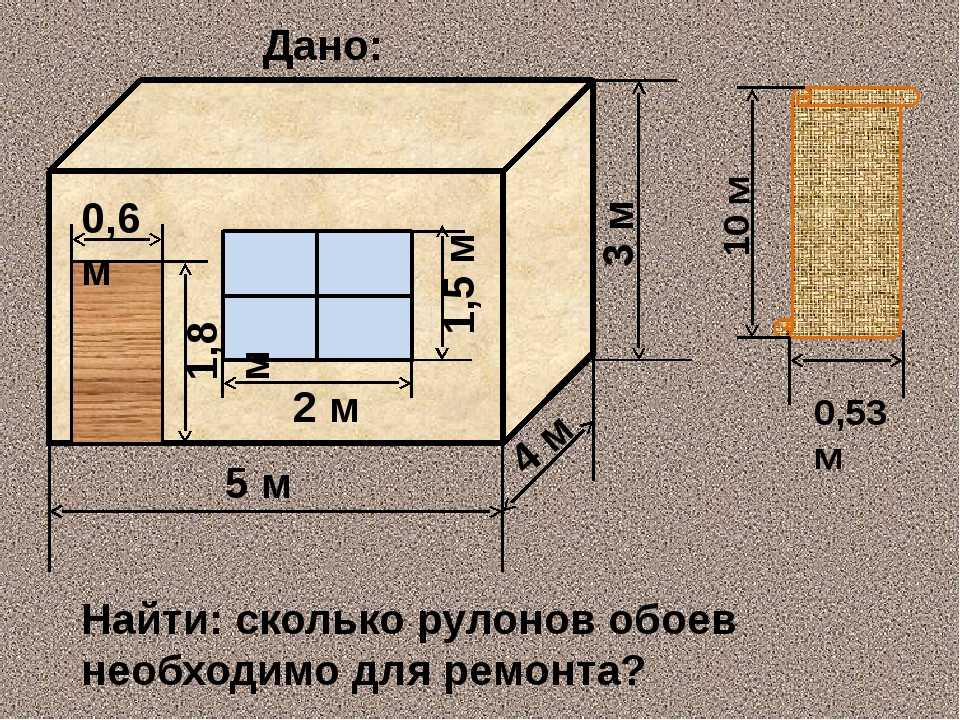 В то же время это высота треугольника, полученного путем проведения линии из вершин восьмиугольника в его центр. Этот треугольник — один из восьми конгруэнтных — является равнобедренным, поэтому его высота может быть рассчитана, например, с помощью теоремы Пифагора по формуле:

h = (1 + √2) × a / 4

Итак, наконец, мы получаем первое уравнение:

Площадь восьмиугольника = периметр * апофема / 2 = (8 × a × (1 + √2) × a / 4) / 2 = 2 × (1 + √2 ) × a²

`Площадь кольца формула`

Кольцо представляет собой кольцеобразный объект – область, ограниченную двумя концентрическими окружностями разного радиуса. Найти площадь по формуле кольца несложно, если вы помните формулу площади круга. Только взгляните: площадь кольца — это разность площадей большего круга радиуса R и меньшего круга радиуса r:

Площадь кольца = πR² - πr² = π(R² - r²)

`Формула площади четырехугольника`

Формула четырехугольника, которую реализует этот калькулятор площади, использует две заданные диагонали и угол между ними.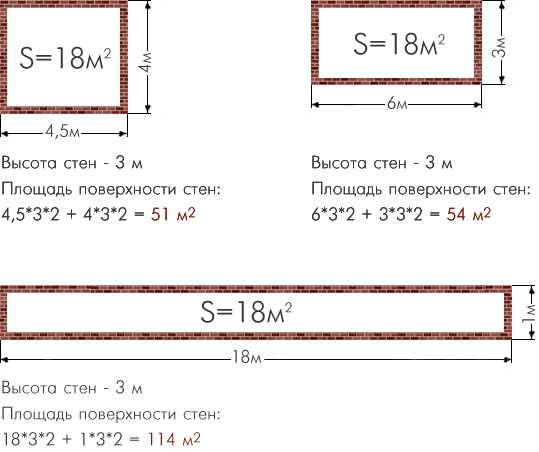

Площадь четырехугольника = e × f × sin(α) , где e и f — диагонали.

Мы можем использовать любой из двух углов при вычислении их синуса. Зная, что два смежных угла дополнительные, можно утверждать, что sin(угол) = sin(180° - угол) .

Если вы ищете другие формулы площади четырехугольника, воспользуйтесь нашим специальным калькулятором четырехугольника, где вы найдете формулу Бретшнайдера (для четырех сторон и двух противоположных углов) и формулу, в которой используются бимедианы и угол между ними. их.

`Формула площади правильного многоугольника`

Формула площади правильного многоугольника выглядит следующим образом:

Площадь правильного многоугольника = n × a² × cot(π/n) / 4

где n — количество сторон, а a — длина стороны.

Существуют и другие уравнения, в которых используются, например, такие параметры, как радиус описанной окружности или периметр. Вы можете найти эти формулы в специальном параграфе нашего калькулятора площади многоугольника.

Если вы имеете дело с неправильным многоугольником, помните, что вы всегда можете разделить фигуру на более простые фигуры, например, на треугольники. Просто посчитайте площадь каждого из них и, в конце, просуммируйте их. Разложение многоугольника на множество треугольников называется триангуляцией многоугольника.

`Часто задаваемые вопросы`

`Какой четырехугольник имеет наибольшую площадь?`

Для данного периметра четырехугольник с максимальной площадью всегда будет квадратом .

`Какая фигура имеет наибольшую площадь при заданном периметре?`

Для заданного периметра замкнутая фигура максимальной площади представляет собой круг .

`Как рассчитать площадь неправильной формы?`

Чтобы вычислить площадь неправильной формы:

Разделите фигуру на несколько частей, для которых можно легко вычислить площадь, например треугольники, прямоугольники, трапеции, (полу)круги и т.