Золотое сечение как рассчитать: Онлайн калькулятор: Золотое сечение

Содержание

Калькулятор золотого сечения (золотой пропорции) онлайн

Золотое сечение — это особое соотношение сторон фигуры, которое наиболее приятно для созерцания. Это число известно с античных времен, а ученые эпохи Возрождения называли его божественной пропорцией. Число Фи — золотое сечение, приблизительно равное 1,618.

История

Особую красоту деления отрезка на стороны в соотношении 1/1,618 заметили еще античные ученые. Евклид в своих началах использовал этот метод при построении пентагона, а пифогорейцы рассматривали весь мир как царство математической гармонии и уделяли большое внимание соотношению 1/1,618. В 1202 году Леонардо Фибоначчи вывел особую последовательность, отношение членов которой стремилось к числу Фибоначчи. Лука Пачоли, один из величайших алгебраистов Италии, назвал это соотношение божественной пропорцией, связав свойства бога с числом Фи. Именно с этого момента золотое сечение начало активно использоваться в работах художников эпохи Возрождения и получило буквально мистический статус. По словам Кеплера, число Фи — бесценная жемчужина математики.

Число Фи в математике

Золотое сечение часто встречается в геометрии. Золотой прямоугольник — фигура на плоскости, длина и ширина которой соотносятся как 1/1,618. Примечательное свойство такого прямоугольника состоит в том, что при удалении из фигуры любого квадрата образуется новый прямоугольник с точно таким же соотношением сторон. Стоит упомянуть и пентаграмму — звездчатый многоугольник, стороны которого пересекаются в соответствии с правилом золотого сечения.

В арифметике число Фи встречается в упоминаемой выше последовательности Фибоначчи, так как lim(Fn/Fn-1) -> Фи. Кроме того, золотое сечение имеет интересное представление в других формах записи. Так, Фи представляется как бесконечная цепочка квадратных корней из единицы. А если привести Фи к цепному виду, то получится бесконечная дробь вида [1; 1, 1, 1, 1, 1…]

Число Фи в реальности

Мистический ореол вокруг золотого сечения возник благодаря такому явлению как «золотой числизм». Энтузиасты, задавшиеся целью найти эту пропорцию в как можно большем количестве реальных объектов или явлений, часто подгоняли результаты. К примеру, храм Парфенон всегда присутствует в списке объектов, которые построены с учетом божественной пропорции. Однако на деле соотношение ширины храма к его высоте составляет 1,74, а если исключить фронтон, то и вовсе 3.

После придания числу божественных свойств, многие художники и музыканты начали сознательно использовать это соотношение в своих работах. Леонардо да Винчи, Альбрехт Дюрер, Иоганн Бах, Ле Корбюзье, Густав Фехнер намеренно придавали своим произведениям форму, соответствующую числу Фи. Одним из современных примеров использования золотого сечения является мозаика Пенроуза — метод непериодического разбиения плоскости.

Несмотря на явное преувеличение свойств золотой пропорции, она все же встречается в реальности. Большинство спиралевидных объектов связны с числом Фи: раковины моллюсков, атмосферные вихри и даже галактики действительно соответствуют божественной пропорции.

Калькулятор золотого сечения

Если вы хотите использовать божественную пропорцию в своей работе, то наш калькулятор к вашим услугам. Для определения сторон золотого прямоугольника вам понадобится ввести одну из сторон, а программа определит вторую, соответствующую правилу золотого сечения. Прелесть калькулятора состоит в том, что он не просто умножает сторону на 1,618, а подбирает целое значение. Именно поэтому вам потребуется оперировать целыми числами, что удобно на практике.

Пример из реальной жизни

Живопись

Допустим, вы хотите сделать приятную с точки зрения математики картину, следовательно, вам нужно нарисовать ее на золотом прямоугольнике. Вам потребуется заказать холст определенного размера, и чтобы определить его размеры, используйте наш калькулятор. Пусть вы хотите писать на холсте, длина которого составит 120 см. Как узнать необходимую ширину? Введите это значение в ячейку A и получите ответ, равный 74 см.

Заключение

Божественная пропорция — мистическое соотношение, которое занимает умы математиков уже несколько тысячелетий. Возможно, именно число Фи содержит ответы на вечные вопросы о тайнах мироздания. Если вам потребуется создать объекты, соответствующие золотому сечению, используйте наш калькулятор, при помощи которого вы сможете подобрать целые числа.

Золотое сечение: Как это работает?


  • Дизайн

  • 4 мин на чтение


  • 145109

Золотое сечение — это универсальное проявление структурной гармонии. Оно встречается в природе, науке, искусстве — во всем, с чем может соприкоснуться человек. Однажды познакомившись с золотым правилом, человечество больше ему не изменяло.

Определение

Наиболее емкое определение золотого сечения гласит, что меньшая часть относится к большей, как большая — ко всему целому. Приблизительная его величина — 1,6180339887. В округленном процентном значении пропорции частей целого будут соотноситься как 62% на 38%. Это соотношение действует в формах пространства и времени.

Древние видели в золотом сечении отражение космического порядка, а Иоганн Кеплер называл его одним из сокровищ геометрии. Современная наука рассматривает золотое сечение как «ассиметричную симметрию», называя его в широком смысле универсальным правилом, отражающим структуру и порядок нашего мироустройства.

История

Представление о золотых пропорциях имели древние египтяне, знали о них и на Руси, но впервые научно золотое сечение объяснил монах Лука Пачоли в книге «Божественная пропорция» (1509), иллюстрации к которой предположительно сделал Леонардо да Винчи. Пачоли усматривал в золотом сечении божественное триединство: малый отрезок олицетворял Сына, большой — Отца, а целое — Святой дух.

Непосредственным образом с правилом золотого сечения связано имя итальянского математика Леонардо Фибоначчи. В результате решения одной из задач ученый вышел на последовательность чисел, известную сейчас как ряд Фибоначчи: 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. На отношение этой последовательности к золотой пропорции обратил внимание Кеплер: «Устроена она так, что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности». Сейчас ряд Фибоначчи — это арифметическая основа для расчетов пропорций золотого сечения во всех его проявлениях.

Леонардо да Винчи также много времени посвятил изучению особенностей золотого сечения, скорее всего, именно ему принадлежит и сам термин. Его рисунки стереометрического тела, образованного правильными пятиугольниками, доказывают, что каждый из полученных при сечении прямоугольников дает соотношения сторон в золотом делении.

Со временем правило золотого сечения превратилось в академическую рутину, и только философ Адольф Цейзинг в 1855 году вернул ему вторую жизнь.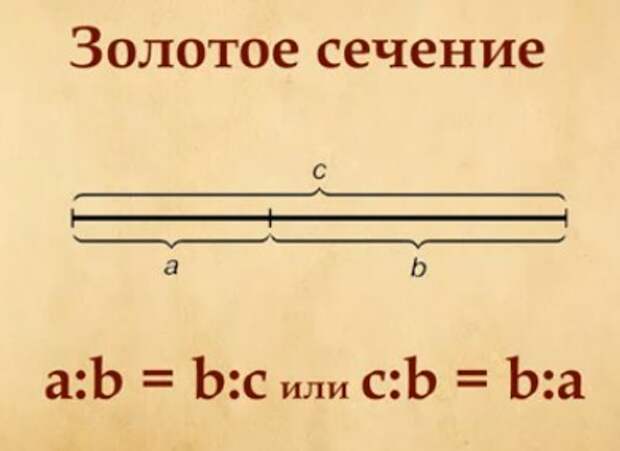 Он довел до абсолюта пропорции золотого сечения, сделав их универсальными для всех явлений окружающего мира. Впрочем, его «математическое эстетство» вызывало много критики.

Природа

Даже не вдаваясь в расчеты, золотое сечение можно без труда обнаружить в природе. Так, под него попадают соотношение хвоста и тела ящерицы, расстояния между листьями на ветке, есть золотое сечение и в форме яйца, если условную линию провести через его наиболее широкую часть.

Белорусский ученый Эдуард Сороко, который изучал формы золотых делений в природе, отмечал, что все растущее и стремящееся занять свое место в пространстве, наделено пропорциями золотого сечения. По его мнению, одна из самых интересных форм это закручивание по спирали.

Еще Архимед, уделяя внимание спирали, вывел на основе ее формы уравнение, которое и сейчас применяется в технике. Позднее Гете отмечал тяготение природы к спиральным формам, называя спираль «кривой жизни». Современными учеными было установлено, что такие проявления спиральных форм в природе как раковина улитки, расположение семян подсолнечника, узоры паутины, движение урагана, строение ДНК и даже структура галактик заключают в себе ряд Фибоначчи.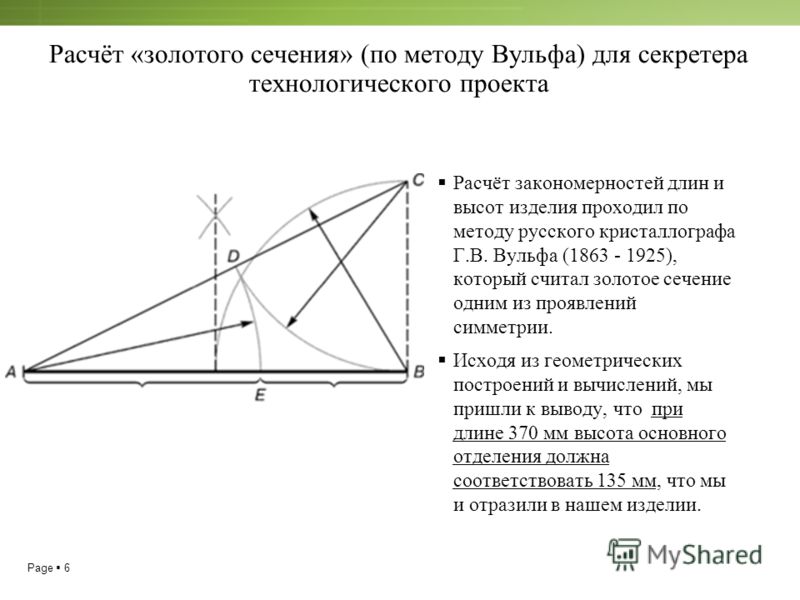

Человек

Модельеры и дизайнеры одежды все расчеты делают, исходя из пропорций золотого сечения. Человек — это универсальная форма для проверки законов золотого сечения. Конечно, от природы далеко не у всех людей пропорции идеальны, что создает определенные сложности с подбором одежды.

В дневнике Леонардо да Винчи есть рисунок вписанного в окружность обнаженного человека, находящегося в двух наложенных друг на друга позициях. Опираясь на исследования римского архитектора Витрувия, Леонардо подобным образом пытался установить пропорции человеческого тела. Позднее французский архитектор Ле Корбюзье, используя «Витрувианского человека» Леонардо, создал собственную шкалу «гармонических пропорций», повлиявшую на эстетику архитектуры XX века.

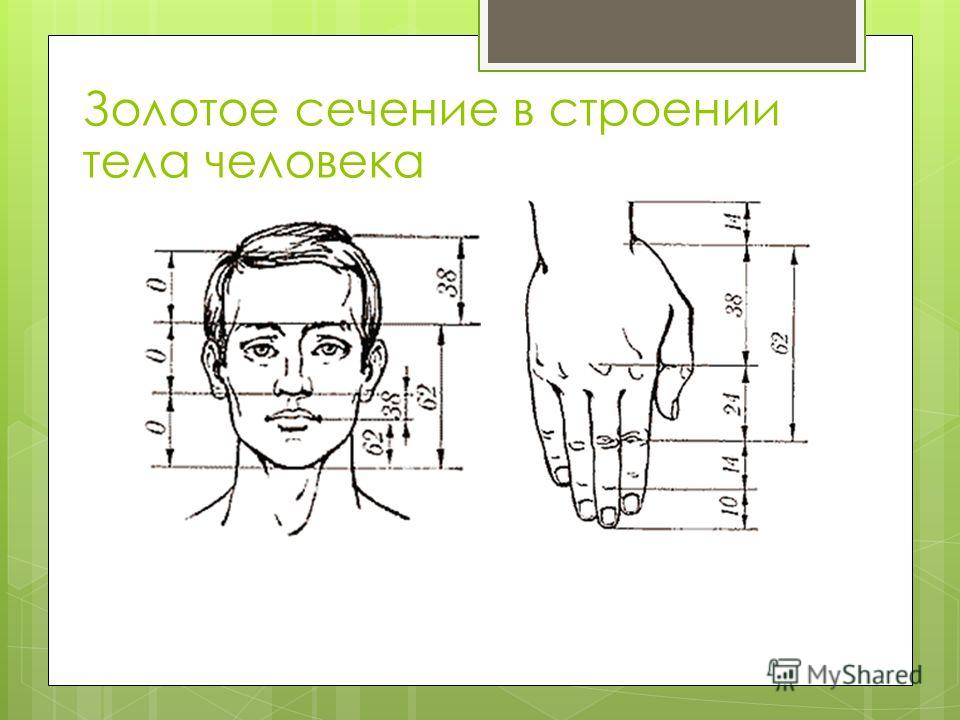
Адольф Цейзинг, исследуя пропорциональность человека, проделал колоссальную работу. Он измерил порядка двух тысяч человеческих тел, а также множество античных статуй и вывел, что золотое сечение выражает среднестатистический закон. В человеке ему подчинены практически все части тела, но главный показатель золотого сечения это деление тела точкой пупа.

В результате измерений исследователь установил, что пропорции мужского тела 13:8 ближе к золотому сечению, чем пропорции женского тела — 8:5.

Искусство пространственных форм

Художник Василий Суриков говорил, «что в композиции есть непреложный закон, когда в картине нельзя ничего ни убрать, ни добавить, даже лишнюю точку поставить нельзя, это настоящая математика». Долгое время художники следовали этому закону интуитивно, но после Леонардо да Винчи процесс создания живописного полотна уже не обходится без решения геометрических задач. Например, Альбрехт Дюрер для определения точек золотого сечения использовал изобретенный им пропорциональный циркуль.

Искусствовед Ф. В. Ковалев, подробно исследовав картину Николая Ге «Александр Сергеевич Пушкин в селе Михайловском», отмечает, что каждая деталь полотна, будь то камин, этажерка, кресло или сам поэт, строго вписаны в золотые пропорции.

Исследователи золотого сечения без устали изучают и замеряют шедевры архитектуры, утверждая, что они стали таковыми, потому что созданы по золотым канонам: в их списке Великие пирамиды Гизы, Собор Парижской Богоматери, Храм Василия Блаженного, Парфенон.

И сегодня в любом искусстве пространственных форм стараются следовать пропорциям золотого сечения, так как они, по мнению искусствоведов, облегчают восприятие произведения и формируют у зрителя эстетическое ощущение.

Слово, звук и кинолента

Формы временно?го искусства по-своему демонстрируют нам принцип золотого деления. Литературоведы, к примеру, обратили внимание, что наиболее популярное количество строк в стихотворениях позднего периода творчества Пушкина соответствует ряду Фибоначчи — 5, 8, 13, 21, 34.

Действует правило золотого сечения и в отдельно взятых произведениях русского классика. Так кульминационным моментом «Пиковой дамы» является драматическая сцена Германа и графини, заканчивающаяся смертью последней.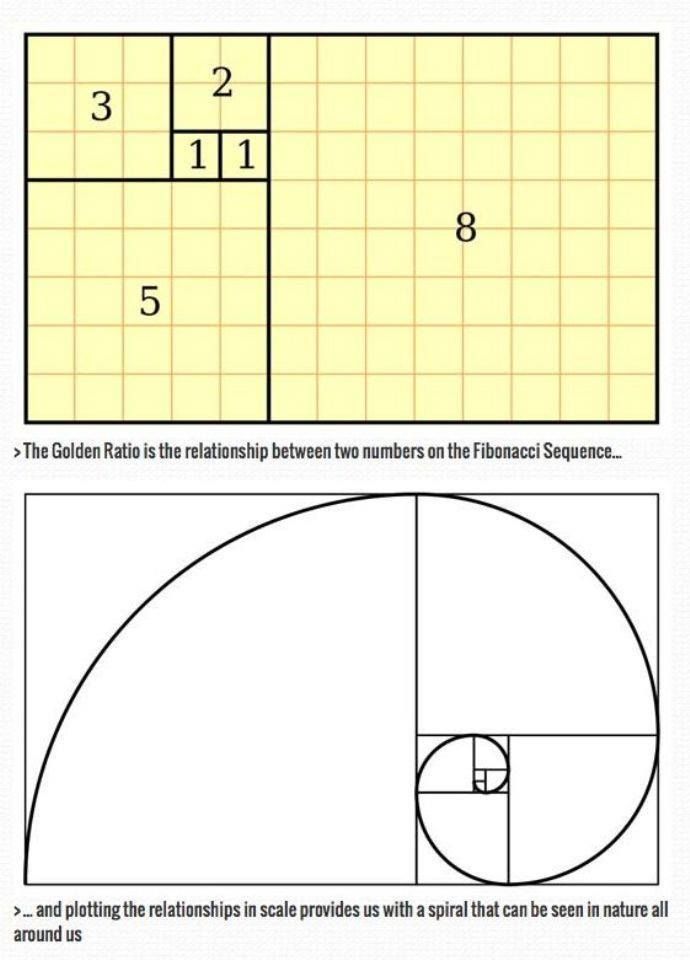 В повести 853 строки, а кульминация приходится на 535 строке (853:535=1,6) — это и есть точка золотого сечения.

Советский музыковед Э. К. Розенов отмечает поразительную точность соотношений золотого сечения в строгих и свободных формах произведений Иоганна Себастьяна Баха, что соответствует вдумчивому, сосредоточенному, технически выверенному стилю мастера. Это справедливо и в отношении выдающихся творений других композиторов, где на точку золотого сечения обычно приходится наиболее яркое или неожиданное музыкальное решение.

Кинорежиссер Сергей Эйзенштейн сценарий своего фильма «Броненосец Потёмкин» сознательно согласовывал с правилом золотого сечения, разделив ленту на пять частей. В первых трех разделах действие разворачивается на корабле, а в последних двух — в Одессе. Переход на сцены в городе и есть золотая середина фильма.

Источник: Academic Painting

  • #дизайн

  • #статья



  • 1


Золотое сечение — что это такое и как его использовать в дизайне

Хороший дизайн обсуждался с тех пор, как мы создаем. Существуют бесконечные форумы, темы в социальных сетях и личные беседы о том, что делает дизайн отличным, и каждый высказывает свою точку зрения.

В этом красота дизайна, верно? Каждый может интерпретировать его по-разному.

Хотя универсального подхода к дизайну никогда не будет, существует конкретный математический подход, который может помочь нам каждый раз становиться на шаг ближе к созданию удивительных дизайнерских решений: золотое сечение.

Золотое сечение — это математическое соотношение, которое можно найти практически везде, например, в природе, архитектуре, живописи и музыке. Когда он применяется специально для дизайна, он создает органичную, сбалансированную и эстетически приятную композицию.

В этой статье мы углубимся в то, что такое золотое сечение, как его рассчитать и как использовать в дизайне, включая удобный список инструментов.

Что такое золотое сечение?

Золотое сечение, также известное как «Золотое сечение», «Золотая середина», «Божественная пропорция» или греческая буква «Фи», представляет собой особое число, приблизительно равное 1,618. Само соотношение исходит из последовательности Фибоначчи, естественной последовательности чисел, которую можно найти повсюду, от количества листьев на дереве до формы морской раковины.

Последовательность Фибоначчи — это сумма двух чисел, стоящих перед ней. Он идет: 0, 1, 1, 2, 3, 5, 8, 13, 21 и так далее до бесконечности. На основе этого шаблона греки разработали золотое сечение, чтобы лучше выразить разницу между любыми двумя числами в последовательности.

Как это связано с дизайном? Вы можете найти золотое сечение, если вы разделите линию на две части, и длинная часть (а), разделенная на меньшую часть (б), равна сумме (а) + (б), деленной на (а), что обе равен 1,618. Эта формула может помочь вам при создании фигур, логотипов, макетов и многого другого.

Вы также можете взять эту идею и создать золотой прямоугольник. Возьмите квадрат и умножьте одну сторону на 1,618, чтобы получить новую форму: прямоугольник с гармоничными пропорциями.

Если вы наложите квадрат на прямоугольник, отношение между двумя фигурами даст вам золотое сечение.

Если вы продолжите применять формулу золотого сечения к новому прямоугольнику в крайнем правом углу, вы получите изображение, состоящее из все более мелких квадратов.

Если вы нарисуете спираль над каждым квадратом, начиная с одного угла и заканчивая противоположным, вы создадите первую кривую последовательности Фибоначчи (также известную как Золотая спираль).

Как использовать золотое сечение в дизайне

Теперь, когда урок математики окончен, как вы можете применить эти знания в повседневной работе?

Вот четыре способа использования золотого сечения в дизайне:

1.

Типография и определение иерархии

Золотое сечение может помочь вам определить, какой размер шрифта вы должны использовать для заголовков и основного текста на веб-сайте, целевой странице, в блоге или даже в печатной кампании.

Допустим, ваш основной текст имеет размер 12 пикселей. Если умножить 12 на 1,618, получится 19..416, что означает, что размер текста заголовка 19px или 20px будет соответствовать золотому сечению и уравновешивать размер основного шрифта 12px.

Если вы хотите выяснить, насколько большим должен быть размер вашего основного текста, вы можете сделать наоборот. Если ваш текст заголовка имеет размер 25 пикселей, вы можете разделить его на 1,618, чтобы найти основной текст (15 или 16 пикселей).

2. Обрезка и изменение размера изображений

При обрезке изображений легко определить пустое пространство, которое нужно вырезать.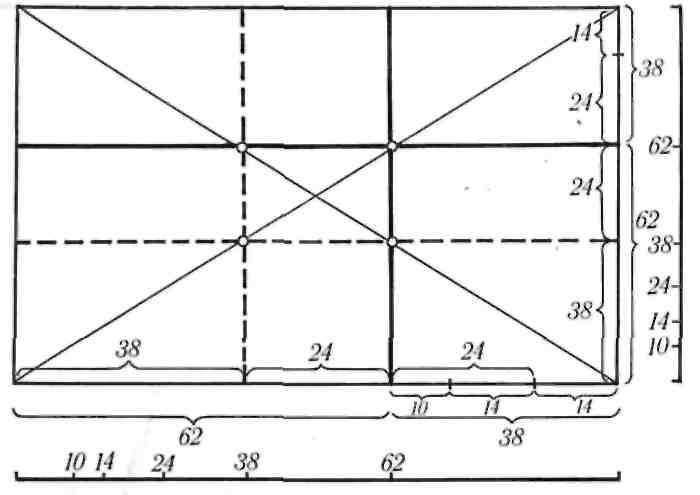 Но как убедиться, что изображение по-прежнему сбалансировано после изменения его размера? Вы можете использовать Золотую спираль в качестве ориентира для композиции изображения.

Например, если вы накладываете Золотую спираль на изображение, вы можете убедиться, что фокус находится в середине спирали.

3. Макет

Использование золотого сечения может помочь вам разработать визуально привлекательный пользовательский интерфейс, который привлекает внимание пользователя к тому, что важнее всего. Например, страница, которая выделяет широкий блок контента слева и более узкий столбец справа, может следовать пропорциям золотого сечения и помочь вам решить, где разместить наиболее важный контент.

4. Разработка логотипа

Если вы разрабатываете новый логотип и чувствуете, что застряли, обратитесь к золотому сечению, чтобы помочь вам набросать пропорции и формы.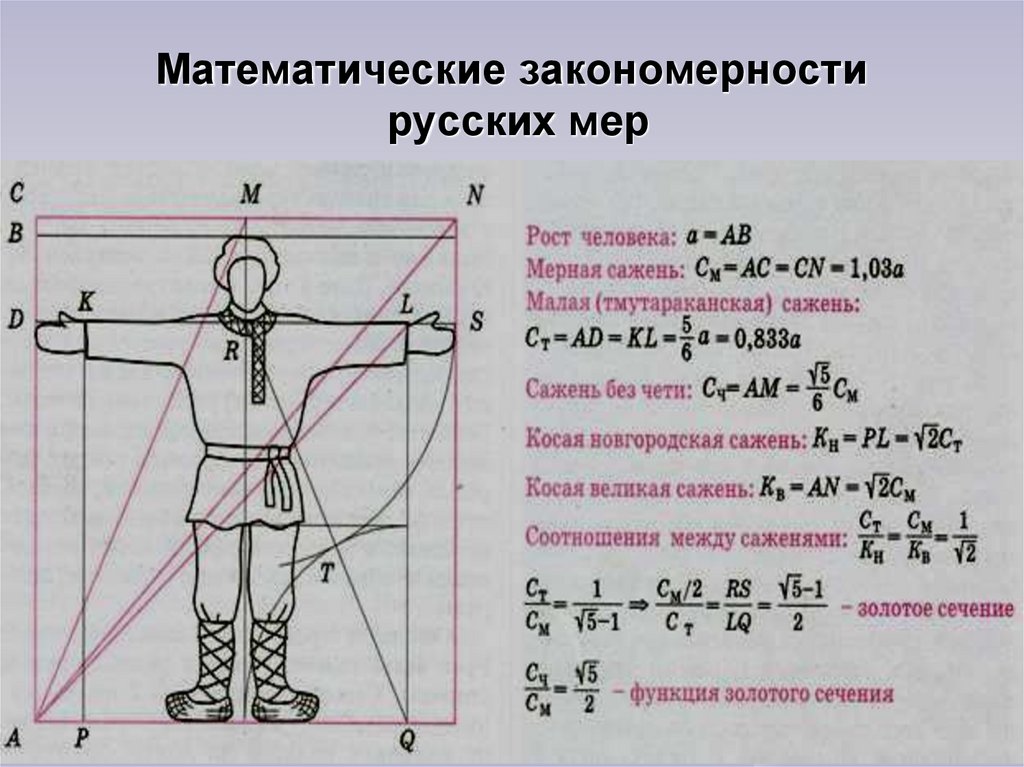 Многие популярные логотипы следуют золотому сечению, например, Twitter, Apple и Pepsi.

Фото: Мостафа Амин и Студия брендологии

Дизайнер Кази Мохаммед Эрфан даже поставил перед собой задачу создать 25 новых логотипов, полностью основанных на золотом сечении. Результат? Простые, сбалансированные и красивые иконки.

Фото: Кази Мохаммед Эрфан

Инструменты, которые помогут вам использовать золотое сечение

Вам не нужно доставать карандаш и бумагу, чтобы вычислить золотое сечение — есть ряд приложений, которые могут сделать это за вас.

Вот пять инструментов, которые помогут вам использовать золотое сечение в своих проектах:

  • Калькулятор золотого сечения: Вычислите более короткую сторону, более длинную сторону и общую длину двух сторон, чтобы вычислить золотое сечение.
  • GoldenRATIO: Созданное для дизайнеров и разработчиков, это приложение позволяет легко создавать веб-сайты, интерфейсы, макеты и многое другое в соответствии с золотым сечением. Он включает в себя встроенный калькулятор с визуальной обратной связью и функции для сохранения положения экрана и настроек, поэтому вам не нужно менять золотое сечение для каждой задачи.
  • Калькулятор типографики золотого сечения: Найдите идеальную типографику для своего веб-сайта, указав размер и ширину шрифта. Вы можете оптимизировать на основе размера шрифта, высоты строки, ширины и количества символов в строке.
  • PhiMatrix : Это программное обеспечение для проектирования и анализа Золотого сечения поставляется с настраиваемыми сетками и шаблонами, которые можно накладывать на любое изображение. Его можно использовать для дизайна и композиции, дизайна продукта, разработки логотипа и многого другого.
  • Ресурс эскиза золотого сечения : Загрузите бесплатный файл эскиза золотой спирали, чтобы помочь с композицией изображения и макета.

Начало работы с золотым сечением

Как только вы узнаете, что искать, вы начнете замечать золотое сечение повсюду. (Не верите? Посмотрите на свои руки. Даже ваши пальцы следуют золотому сечению.) Человеческий глаз привык видеть это магическое число, и мы подсознательно реагируем на него положительно.

Как дизайнеры, мы можем использовать это число в своих интересах. Даже небольшие изменения в том, как вы обрезаете изображение или разрабатываете макет, могут значительно улучшить взаимодействие пользователей с вашим дизайном.

Смотрите прямо сейчас.

Эмили Эспозито

Эмили писала для некоторых ведущих технологических компаний, охватывая все, от творческого копирайтинга до UX-дизайна.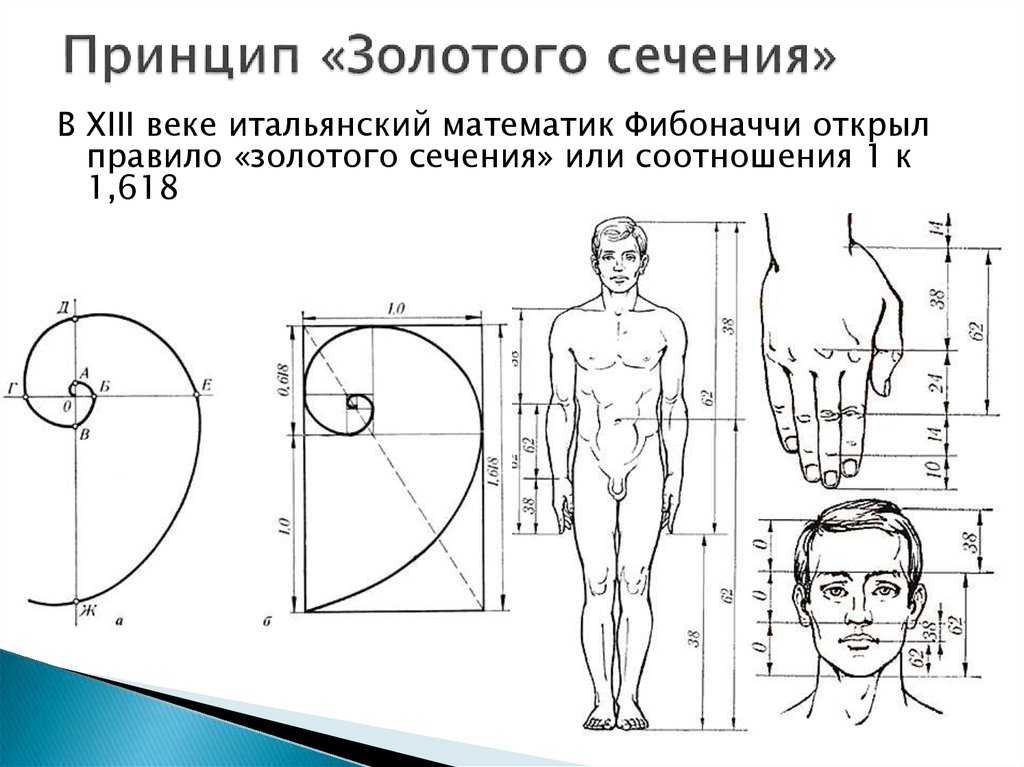 Когда она не пишет, она путешествует по миру (следующая остановка: Япония!), варит чайный гриб и катается на велосипеде по северо-западу Тихого океана.

Калькулятор золотого сечения

Создано Петром Малеком и Матеушем Мухой

Отредактировано Богной Шик и Джеком Боуотером

Последнее обновление: 28 марта 2023 г.

Содержание:

  • Что такое золотое сечение?
  • Золотой прямоугольник
  • Часто задаваемые вопросы

Калькулятор золотого сечения рассчитает более короткую сторону, большую сторону и общую длину двух сторон, чтобы вычислить золотое сечение . Прежде чем мы сможем рассчитать золотое сечение, важно ответить на вопрос: «Что такое золотое сечение?». Следующая статья надеется дать вам ответ.

Вы также можете воспользоваться калькулятором пропорций, если хотите анализировать пропорции в целом.

Что такое золотое сечение?

Золотое сечение, также известное как золотое сечение или золотая пропорция, получается, когда длины двух отрезков имеют такое же отношение, как отношение их суммы к большей из двух длин.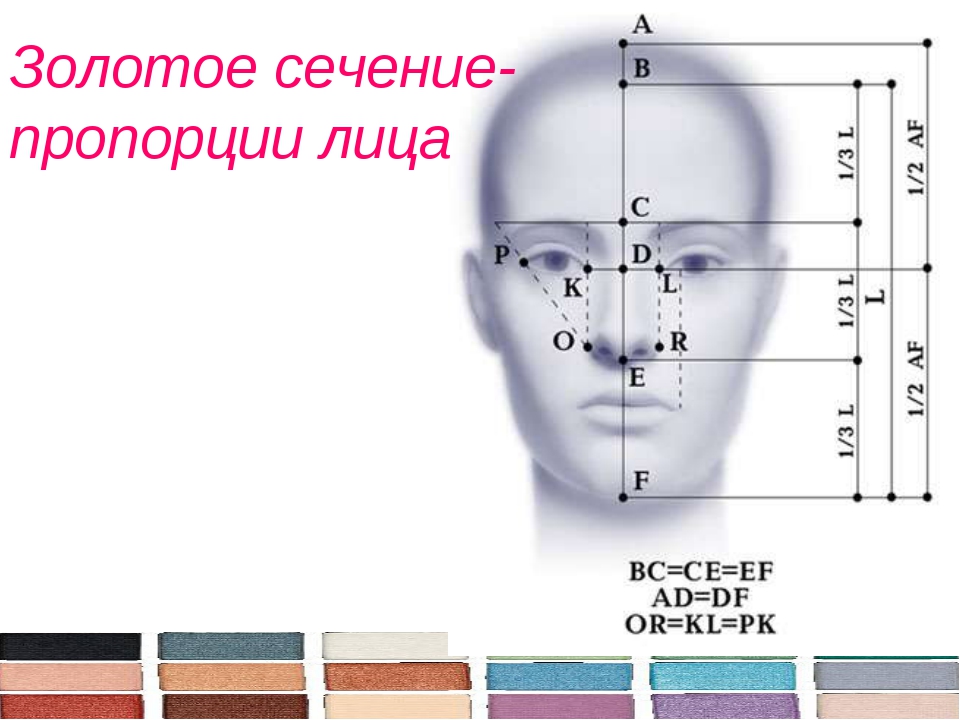 Значение золотого сечения, которое является пределом отношения последовательных чисел Фибоначчи, имеет значение приблизительно 1,6181,6181,618.

Формула золотого сечения выглядит следующим образом. Пусть больший из двух отрезков будет aaa, а меньший обозначим как bbb Тогда золотое сечение равно (a+b)/a=a/b\small (a+b)/a = a/b(a+b )/a=a/b Любой старый калькулятор соотношений сделает этот трюк за вас, но этот калькулятор золотого сечения решает эту проблему специально, так что вам не о чем беспокоиться!

Вот пошаговый метод решения соотношения вручную.

  1. Найдите более длинный сегмент и обозначьте его как aaa.

  2. Найдите более короткий сегмент и назовите его bbb.

  3. Введите значения в формулу.

  4. Возьмите сумму aaa и bbb и разделите на aaa.

  5. Разделить aaa на bbb.

  6. Если пропорция находится в золотом сечении, она будет равна примерно 1,6181,6181,618.

  7. Используйте калькулятор золотого сечения, чтобы проверить результат.

Калькулятор постулата сложения сегментов можно использовать для нахождения одной из длин сегментов, когда 3 точки лежат на одной прямой и известны два расстояния.

Золотой прямоугольник

Золотой прямоугольник — это прямоугольник длиной a+ba+ba+b и шириной aaa. Этот прямоугольник часто можно увидеть в искусстве, так как было сказано, что он самый приятный для глаз из всех подобных прямоугольников. Калькулятор золотого прямоугольника — это удобный способ найти золотой прямоугольник вместо того, чтобы работать с ним вручную.

Золотое сечение встречается во многих формах архитектуры и в некоторых природных узорах, например, в расположении листьев у некоторых растений. Золотая пропорция также наблюдается в правильных пятиугольниках. Вы можете найти больше информации об этой форме в калькуляторе пятиугольника.

Часто задаваемые вопросы

Что такое золотое сечение?

Золотое сечение — это отношение между двумя величинами, которое мы также можем найти, вычислив отношение между суммой этих величин и большей из двух .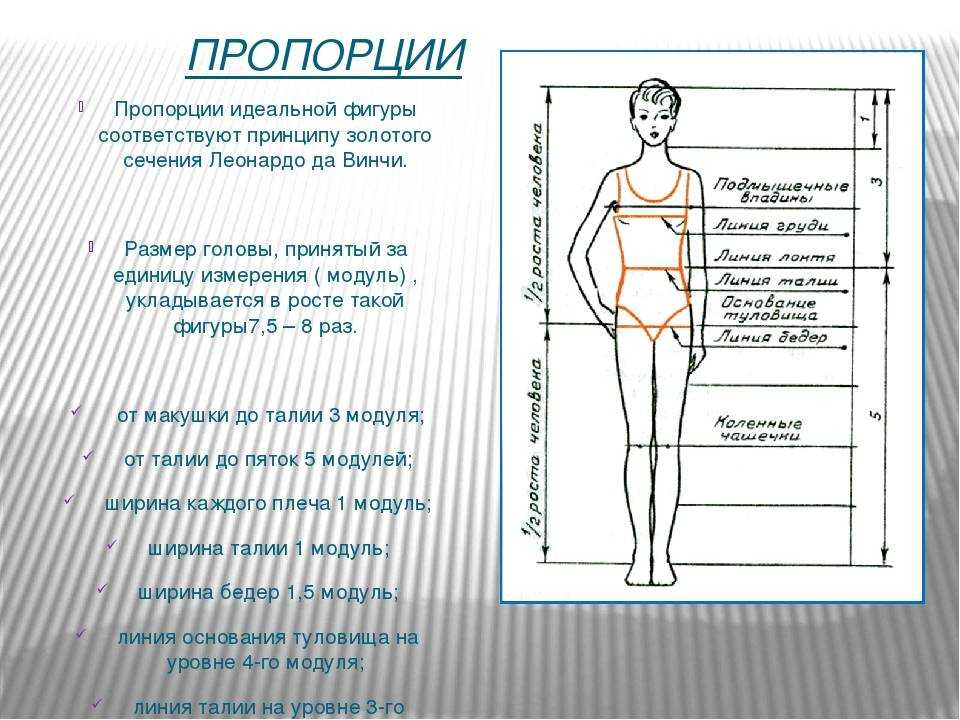 Численно говоря, числа a и b находятся в золотом сечении, если:

a/b = (a + b)/a

Это отношение имеет определенное значение, обозначаемое греческой буквой φ :

φ = 1,618033988749

Золотое сечение высоко ценится, поскольку фигуры, построенные в соответствии с этими пропорциями, выглядят особенно приятными для человеческого глаза.

Какова длина сторон золотого прямоугольника с диагональю 1?

Стороны золотого прямоугольника с диагональю d = 1 равны a = 0,850651 и b = 0,525731 . Чтобы найти эти результаты:

  1. Используйте теорему Пифагора, чтобы найти длину стороны b как функцию a :

    b = кв.(1 - a²) .

  2. Вычислите длину стороны a , зная, что a/b = φ :

    а/б = φ
    a/sqrt(1 - a²) - φ
    a = sqrt(φ²/(1 + φ²)) = 0,850651

  3. Вычислите длину стороны b по следующей формуле:

    b = а/φ = 0,525731

Вот оно!

Почему золотое сечение важно?

Золотое сечение всегда имело особое значение в науке и искусстве благодаря своим свойствам и внешнему виду.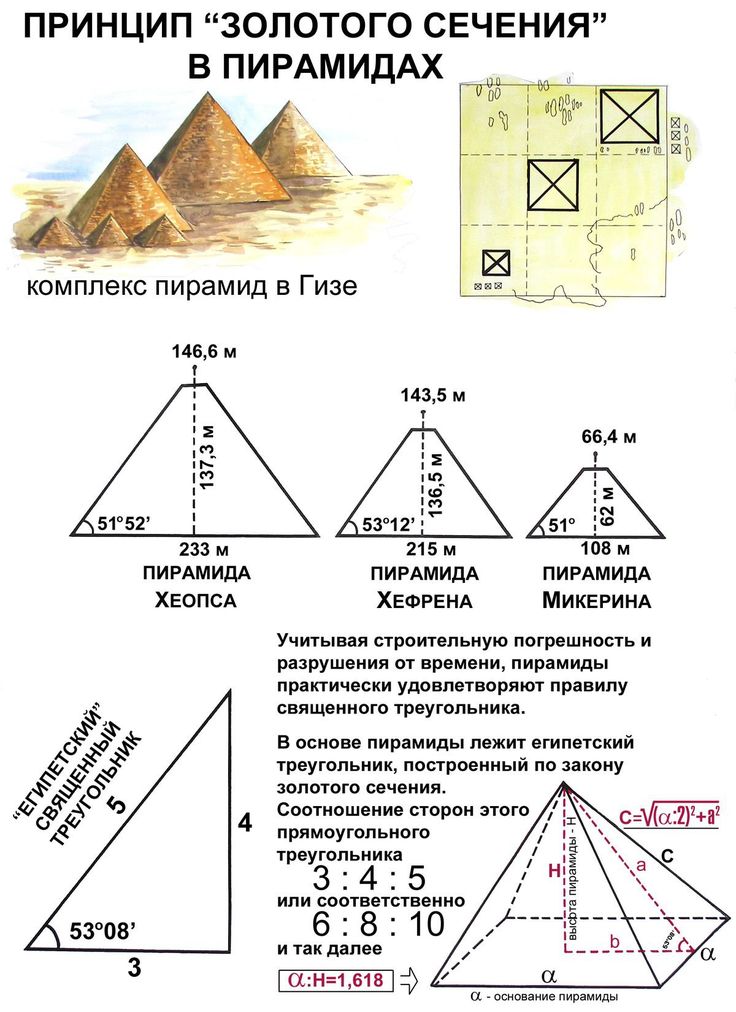 К слову о математике:

  • Золотой прямоугольник (прямоугольник со сторонами в золотом сечении) можно разделить на два меньших золотых прямоугольника (соотношение сохраняется).
  • Золотое сечение тесно связано с числом 5 . Это число появляется в его определении ( φ = (1 + √5)/2 ) и пятиугольника как отношение между диагональю и стороной.

В искусстве золотое сечение появилось сравнительно недавно: Дали, например, использовал это соотношение в своих работах.

Где найти золотое сечение в природе?

Многие источники, как исторические, так и современные, утверждают, что золотое сечение довольно распространено в природе. Некоторые примеры:

  • Характер роста листьев;
  • Геометрические поверхности некоторых овощей и ракушек;
  • Пропорции костей некоторых животных.

Однако, хотя мы не можем отрицать наличие геометрических узоров в природе, мы не можем подтвердить точность пропорций приведенных выше примеров: некоторые из них имеют огромные вариации, а другие лишь приближаются к золотому сечению.