Содержание
Калькулятор золотого сечения (золотой пропорции) онлайн
Золотое сечение — это особое соотношение сторон фигуры, которое наиболее приятно для созерцания. Это число известно с античных времен, а ученые эпохи Возрождения называли его божественной пропорцией. Число Фи — золотое сечение, приблизительно равное 1,618.
История
Особую красоту деления отрезка на стороны в соотношении 1/1,618 заметили еще античные ученые. Евклид в своих началах использовал этот метод при построении пентагона, а пифогорейцы рассматривали весь мир как царство математической гармонии и уделяли большое внимание соотношению 1/1,618. В 1202 году Леонардо Фибоначчи вывел особую последовательность, отношение членов которой стремилось к числу Фибоначчи. Лука Пачоли, один из величайших алгебраистов Италии, назвал это соотношение божественной пропорцией, связав свойства бога с числом Фи. Именно с этого момента золотое сечение начало активно использоваться в работах художников эпохи Возрождения и получило буквально мистический статус.
По словам Кеплера, число Фи — бесценная жемчужина математики.
Число Фи в математике
Золотое сечение часто встречается в геометрии. Золотой прямоугольник — фигура на плоскости, длина и ширина которой соотносятся как 1/1,618. Примечательное свойство такого прямоугольника состоит в том, что при удалении из фигуры любого квадрата образуется новый прямоугольник с точно таким же соотношением сторон. Стоит упомянуть и пентаграмму — звездчатый многоугольник, стороны которого пересекаются в соответствии с правилом золотого сечения.
В арифметике число Фи встречается в упоминаемой выше последовательности Фибоначчи, так как lim(Fn/Fn-1) -> Фи. Кроме того, золотое сечение имеет интересное представление в других формах записи. Так, Фи представляется как бесконечная цепочка квадратных корней из единицы. А если привести Фи к цепному виду, то получится бесконечная дробь вида [1; 1, 1, 1, 1, 1…]
Число Фи в реальности
Мистический ореол вокруг золотого сечения возник благодаря такому явлению как «золотой числизм».
Энтузиасты, задавшиеся целью найти эту пропорцию в как можно большем количестве реальных объектов или явлений, часто подгоняли результаты. К примеру, храм Парфенон всегда присутствует в списке объектов, которые построены с учетом божественной пропорции. Однако на деле соотношение ширины храма к его высоте составляет 1,74, а если исключить фронтон, то и вовсе 3.
После придания числу божественных свойств, многие художники и музыканты начали сознательно использовать это соотношение в своих работах. Леонардо да Винчи, Альбрехт Дюрер, Иоганн Бах, Ле Корбюзье, Густав Фехнер намеренно придавали своим произведениям форму, соответствующую числу Фи. Одним из современных примеров использования золотого сечения является мозаика Пенроуза — метод непериодического разбиения плоскости.
Несмотря на явное преувеличение свойств золотой пропорции, она все же встречается в реальности. Большинство спиралевидных объектов связны с числом Фи: раковины моллюсков, атмосферные вихри и даже галактики действительно соответствуют божественной пропорции.
Калькулятор золотого сечения
Если вы хотите использовать божественную пропорцию в своей работе, то наш калькулятор к вашим услугам. Для определения сторон золотого прямоугольника вам понадобится ввести одну из сторон, а программа определит вторую, соответствующую правилу золотого сечения. Прелесть калькулятора состоит в том, что он не просто умножает сторону на 1,618, а подбирает целое значение. Именно поэтому вам потребуется оперировать целыми числами, что удобно на практике.
Пример из реальной жизни
Живопись
Допустим, вы хотите сделать приятную с точки зрения математики картину, следовательно, вам нужно нарисовать ее на золотом прямоугольнике. Вам потребуется заказать холст определенного размера, и чтобы определить его размеры, используйте наш калькулятор. Пусть вы хотите писать на холсте, длина которого составит 120 см. Как узнать необходимую ширину? Введите это значение в ячейку A и получите ответ, равный 74 см.
Заключение
Божественная пропорция — мистическое соотношение, которое занимает умы математиков уже несколько тысячелетий.
Возможно, именно число Фи содержит ответы на вечные вопросы о тайнах мироздания. Если вам потребуется создать объекты, соответствующие золотому сечению, используйте наш калькулятор, при помощи которого вы сможете подобрать целые числа.
Калькулятор «золотого сечения»
- Главная
- Калькуляторы
- Математика
- Числа
- Калькулятор «золотого сечения»
Золотое сечение или Божественная Пропорция были тщательно изучены
греческим скульптором и архитектором Фидием. Созданное самой природой
правило принято обозначать в честь его открывателя буквой Ф.
Фи может быть обнаружено по всей вселенной — от спиралей галактик до
спирали раковины Наутилуса. В геометрии золотое сечение можно
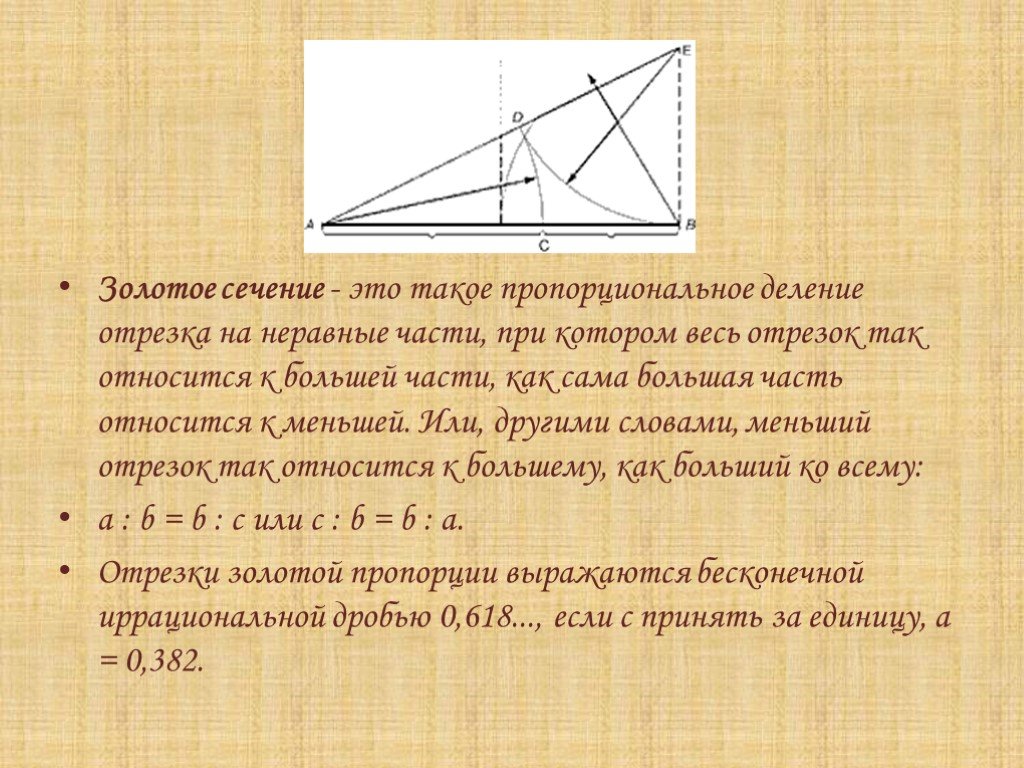
представить как отрезок C состоящий из двух неравных частей. При этом его меньшая часть A составляет такую же долю в большем отрезке B, как и больший отрезок B занимает во всем отрезке C.
В математическом виде правило выглядит так:
ABC
A + B = C
A / B = B / C
C / B = B / A
Введите один из известных размеров и калькулятор золотого сечения вычислит остальные:
Точность:
В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Числа
Калькулятор
Расчёт
Уравнение
Математика
19966
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
Треугольник Паскаля
Числа Калькулятор Расчёт Математика Формулы
Тетраэдрические числа
Числа Калькулятор Расчёт Математика
Пентагональные числа
Числа Калькулятор Расчёт Математика
Простые числа
Числа Калькулятор Расчёт Математика
Гармонический треугольник Лейбница
Числа Калькулятор Генератор Математика Формулы
Последовательность Кимберлинга
Числа Калькулятор Расчёт Множества Математика
Конвертер чисел в римские цифры
Числа Калькулятор Конвертер Преобразовать Математика
Преобразование числа в другие значения
Числа Калькулятор Числа
Основные тригонометрические тождества
Тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла, которая позволяет находить любую из данных функций при условии, что будет известна какая-либо другая.
Тригонометрия Математика Тригонометрия Формулы Теория
Калькулятор калорий для похудения онлайн
Калькуляторы веса и калорий Калькулятор Расчёт
Размеры форматов листов А5, А4, А3, А2, А1, А0 в миллиметрах и мегабайтах
Разное Размеры
Сколько в ампере ватт, как перевести амперы в ватты и киловатты
Мощность – это скорость расходования энергии, выраженная в отношении энергии ко времени: 1 Вт = 1 Дж/1 с. Один ватт равен отношению одного джоуля (единице измерения работы) к одной секунде.
Электротехника Формулы Физика Теория Электричество
Назначение и структура операционных систем
Операционные системы Информатика
Калькулятор идеального веса
Калькуляторы веса и калорий Калькулятор Расчёт
Что такое Ом
1 ом представляет собой электрическое сопротивление между двумя точками проводника, когда постоянная разность потенциалов 1 вольт, приложенная к этим точкам, создаёт в проводнике ток 1 ампер, а в проводнике не действует какая-либо электродвижущая сила.
Электротехника Формулы Физика Теория Электричество
Сколько грамм в ложке
Масса и вес Масса Физика Теория Единицы измерения
Золотое сечение — определение, формула, примеры
Золотое сечение, которое часто называют золотым сечением, божественной пропорцией или золотым сечением, представляет собой особый атрибут, обозначаемый символом ϕ, и примерно равен 1,618. Изучение многих специальных формаций может быть выполнено с использованием специальных последовательностей, таких как последовательность Фибоначчи, и атрибутов, таких как золотое сечение.
Это соотношение встречается в различных искусствах, архитектуре и дизайне. Многие замечательные архитектурные сооружения, такие как Великая пирамида Египта, Парфенон, были частично или полностью спроектированы так, чтобы отражать в своей структуре золотое сечение. Великие художники, такие как Леонардо да Винчи, использовали золотое сечение в нескольких своих шедеврах, и в 1500-х годах оно было известно как «Божественная пропорция».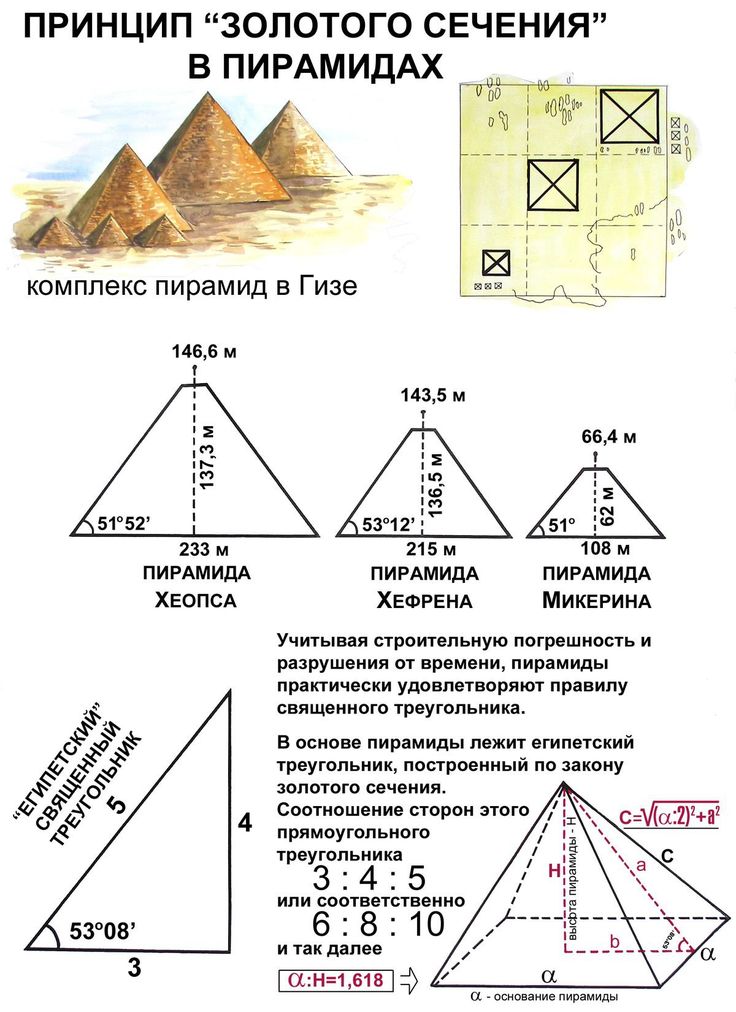
Давайте узнаем больше о золотом сечении в этом уроке.
| 1. | Что такое золотое сечение? |
| 2. | Формула золотого сечения |
| 3. | Как рассчитать золотое сечение? |
| 4. | Что такое золотой прямоугольник? |
| 5. | Что такое последовательность Фибоначчи? |
| 6. | Часто задаваемые вопросы о золотом сечении |
Что такое золотое сечение?
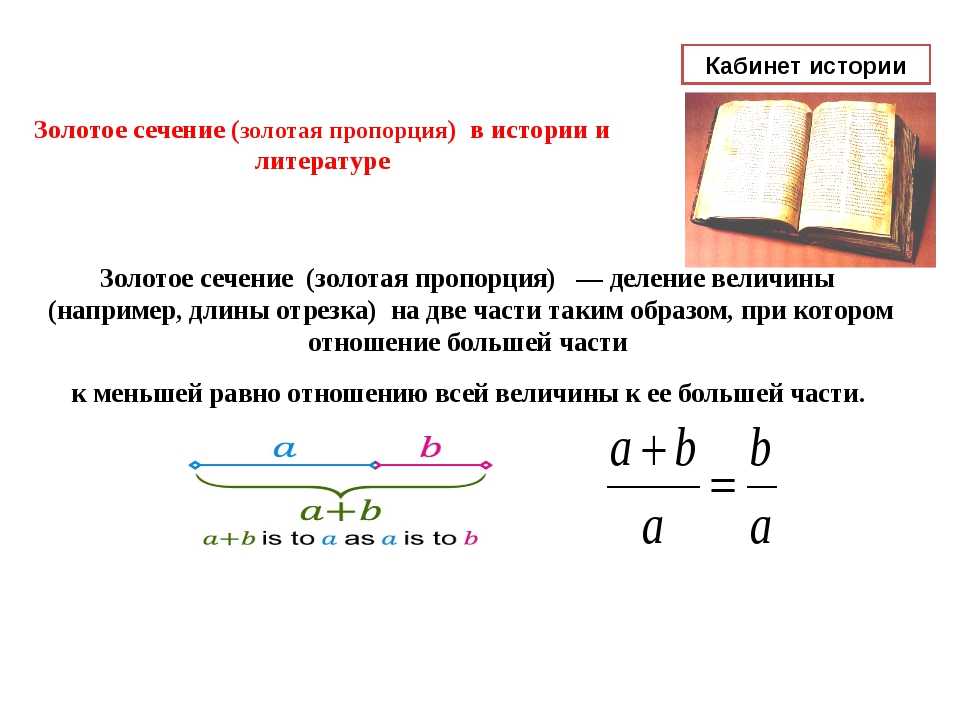
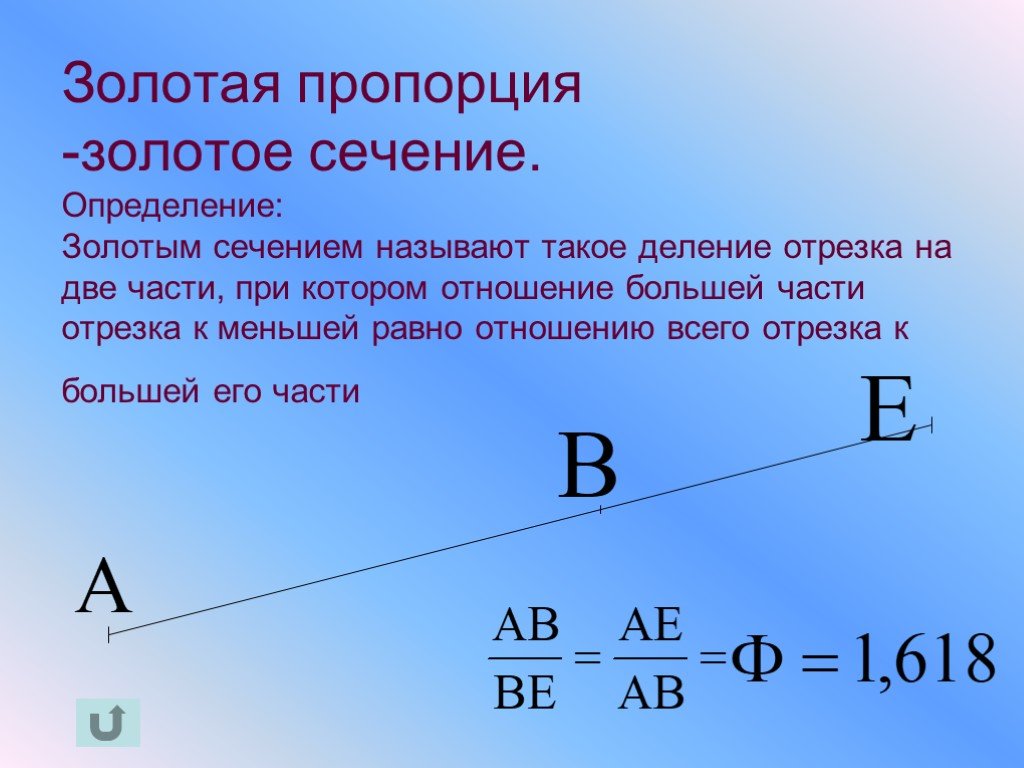
Золотое сечение, также называемое золотым сечением, божественной пропорцией или золотым сечением, существует между двумя величинами, если их отношение равно отношению их суммы к большей величине между ними. Со ссылкой на это определение, если мы разделим линию на две части, части будут в золотом сечении, если:
Отношение длины более длинной части, скажем, «а», к длине более короткой части, скажем, «b» равно отношению их суммы «(a + b)» к большей длине.
Обратитесь к следующей диаграмме для лучшего понимания вышеуказанной концепции:
Обозначается греческой буквой ϕ, произносимой как «фи». Приблизительное значение ϕ равно 1,61803398875 . Оно находит применение в геометрии, искусстве, архитектуре и других областях. Таким образом, следующее уравнение устанавливает соотношение для расчета золотого сечения: два.
Определение золотого сечения
Когда линия делится на две части, длинная часть, которая делится на короткую часть, равна всей длине, деленной на длинную часть, определяется как золотое сечение. Ниже приведены примеры золотого сечения в архитектуре и искусстве.
Существует множество применений золотого сечения в области архитектуры. Многие архитектурные чудеса, такие как Великая мечеть Кайруана, были построены с учетом золотого сечения в их структуре. Такие художники, как Леонардо да Винчи, Рафаэль, Сандро Боттичелли и Жорж Сера, использовали это как атрибут в своих работах.
Формула золотого сечения
Формулу золотого сечения можно использовать для расчета значения золотого сечения. Уравнение золотого сечения выведено, чтобы найти общую формулу для расчета золотого сечения.
Уравнение золотого сечения
Из определения золотого сечения
a/b = (a + b)/a = ϕ
Из этого уравнения получаем два уравнения:
a/b = ϕ → ( 1)
(а + b)/а = ϕ → (2)
Из уравнения (1)
a/b = ϕ
⇒ a = b
Подставить это в уравнение (2):
(bϕ + b)/bϕ = ϕ
b( ϕ + 1)/ bϕ = ϕ
(ϕ + 1)/ϕ = ϕ
1 + 1/ϕ = ϕ
1 + 1/ϕ = ϕ
Как рассчитать золотое сечение?
Значение золотого сечения можно рассчитать разными методами. Начнем с основного.
Метод проб и ошибок
Мы угадаем произвольное значение константы, а затем выполним следующие шаги, чтобы вычислить более близкое значение на каждой итерации.
- Вычислите мультипликативную обратную величину угаданного вами значения, т. е. 1/значение. Это значение будет нашим первым термином.
- Вычислите другой член, добавив 1 к мультипликативному, обратному этому значению.
- Оба условия, полученные на предыдущих шагах, должны быть равны. Если нет, мы будем повторять процесс, пока не получим примерно равное значение для обоих членов.
- Для второй итерации мы будем использовать предполагаемое значение, равное члену 2, полученному на шаге 2, и так далее.
е. 1/значение. Это значение будет нашим первым термином.Например,
Поскольку ϕ = 1 + 1/ϕ, оно должно быть больше 1. Начнем со значения 1,5 в качестве нашего первого предположения.
- Член 1 = Мультипликативное обратное 1,5 = 1/1,5 = 0,6666…
- Член 2 = мультипликативный, обратный 1,5 + 1 = 0,6666.. + 1 = 1,6666…
Поскольку оба термина не равны, мы повторим этот процесс снова, используя предполагаемое значение, равное термину 2 .
В следующей таблице приведены данные расчетов для всех принятых значений, пока мы не получим желаемые равные условия:
| Итерация | Предполагаемое значение | Термин 1 (1/значение) | Термин 2 (1/значение + 1) |
|---|---|---|---|
1. | 1,5 | 11,511,5 = 0,6666.. | 0,6666.. + 1 = 1,6666.. |
| 2. | 1.6666.. | 11,666..11,666.. = 0,6 | 0,6 + 1 = 1,6 |
| 3. | 1,6 | 11,611,6 = 0,625 | 0,625 + 1 = 1,625 |
| 4. | 1,625 | 11,62511,625 = 0,61538.. | 0,61538.. + 1 = 1,61538.. |
| 5. | 1.61538.. | .. | .. и так далее |
Чем больше итераций вы выполните, тем ближе приблизительное значение будет к точному. Другие методы обеспечивают более эффективный способ вычисления точного значения. 92 — 4ac}}{2a}\)
Подставляя значения a = 1, b = -1 и c = -1, получаем
ϕ = \(\frac{1 \pm \sqrt{( 1 + 4 )}}{2}\)
Решение можно упростить до положительного значения, что даст:
ϕ = 1/2 + √5/2
Обратите внимание, что мы не рассматриваем отрицательное значение, так как \( \phi\) — это отношение длин, и оно не может быть отрицательным.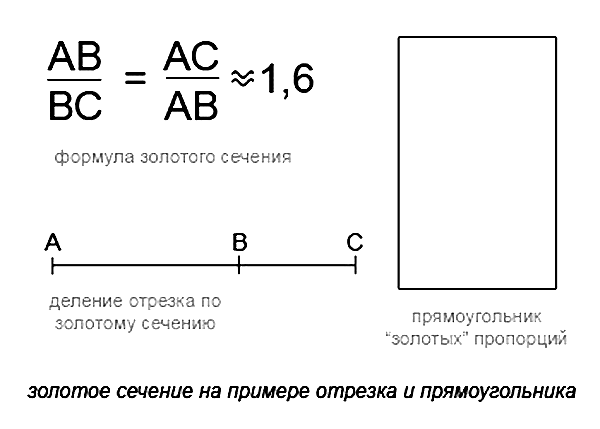
Следовательно, ϕ = 1/2 + √5/2
Что такое золотой прямоугольник?
В геометрии золотой прямоугольник определяется как прямоугольник, длины сторон которого находятся в золотом сечении. Золотой прямоугольник демонстрирует совершенно особую форму самоподобия. Все прямоугольники, созданные путем добавления или удаления квадрата, также являются золотыми прямоугольниками.
Построение золотого прямоугольника
Мы можем построить золотой прямоугольник, выполнив следующие шаги:
- Шаг 1: Сначала мы нарисуем квадрат со стороной 1 единица. На одной из его сторон нарисуйте точку посередине. Теперь мы проведем линию от этой точки до угла другой стороны.
- Шаг 2: Используя эту линию в качестве радиуса и точку, проведенную посередине, в качестве центра, нарисуйте дугу, идущую вдоль стороны квадрата. Длину этой дуги можно рассчитать с помощью теоремы Пифагора: √(1/2) 2 + (1) 2 = √5/2 шт.
- Шаг 3: Используйте пересечение этой дуги и стороны квадрата, чтобы нарисовать прямоугольник, как показано на рисунке ниже:
Это золотой прямоугольник, потому что его размеры находятся в золотом сечении. т. е. ϕ = (√5/2 + 1/2)/1 = 1,61803
Что такое последовательность Фибоначчи?
Последовательность Фибоначчи — это особый ряд чисел, в котором каждый член (начиная с третьего члена) является суммой двух предыдущих членов. Для нахождения последовательности Фибоначчи можно использовать следующие шаги:
- Начнем с того, что возьмем 0 и 1 в качестве первых двух членов.
- Таким образом, третий член 1 вычисляется путем сложения 0 и 1.
- Точно так же следующий член = 1 + 2 = 3 и так далее.
Последовательность Фибоначчи задается как 0, 1, 1, 2, 3, 5, 8, 13, 21,… и так далее. Последовательность Фибоначчи и золотое сечение имеют между собой особую связь. Когда мы начинаем вычислять отношения двух последовательных членов ряда Фибоначчи, значение каждого последующего отношения становится ближе к точному значению ϕ.
Например,
В следующей таблице показаны значения соотношений, максимально приближающиеся к значению ϕ. В следующей таблице показаны значения соотношений, максимально приближающиеся к значению ϕ.
| Срок 1 | Срок 2 | Соотношение = Клемма 2 / Клемма 1 |
|---|---|---|
| 2 | 3 | 1,5 |
| 3 | 5 | 1.6666.. |
| 5 | 8 | 1,6 |
| 8 | 13 | 1,625 |
| 13 | 21 | 1.61538 |
☛Связанные темы
Ниже приведен список тем, тесно связанных с золотым сечением. Эти темы также дадут вам представление о том, как такие понятия рассматриваются в Cuemath.
- Среднее
- Соотношение
- Числа Фибоначчи
- Квадратные уравнения
- Соотношение, доля, процентные формулы
Часто задаваемые вопросы о золотом сечении
Что такое золотое сечение простыми словами?
Золотое сечение — это математическое отношение, которое существует между двумя величинами, если их отношение равно отношению их суммы к большей из них величин.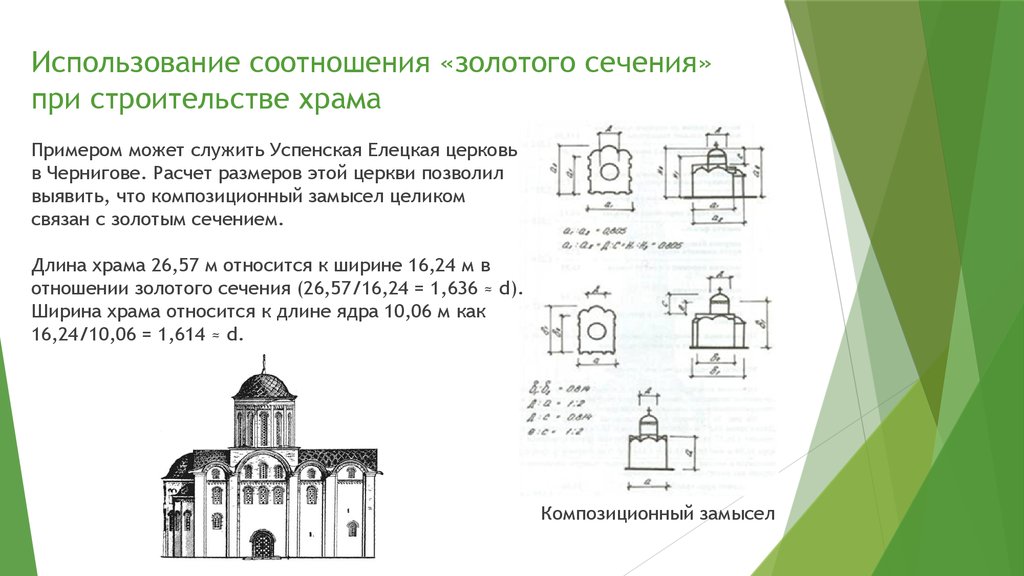
Другими словами, когда линия разделена на две части и более длинная часть «а», разделенная на меньшую часть «b», равна сумме (а + b), деленной на «а», это означает, что линия отражая золотое сечение, которое равно 1,618.
Что вы подразумеваете под золотым прямоугольником?
В геометрии золотой прямоугольник определяется как прямоугольник, длины сторон которого находятся в золотом сечении. Золотой прямоугольник демонстрирует совершенно особую форму самоподобия. Все прямоугольники, созданные путем добавления или удаления квадрата, также являются золотыми прямоугольниками.
Почему золотое сечение красиво?
Золотое сечение — это соотношение, которое при использовании в различных областях для проектирования объектов делает объекты эстетически привлекательными и приятными на вид. Поэтому золотое сечение называют красивым атрибутом. Его можно заметить в различных узорах природы, например, в спиралевидном расположении цветов и листьев. Есть много применений золотого сечения в области архитектуры.
Многие архитектурные чудеса были построены, чтобы отразить золотое сечение в своей структуре, например, Великая пирамида Египта и Великая мечеть Кайруана.
Почему золотое сечение важно?
Золотое сечение — это математическое соотношение, которое часто встречается в природе и используется в различных областях. Он используется в нашей повседневной жизни, искусстве и архитектуре. Объекты, созданные с учетом золотого сечения в своей структуре и дизайне, более приятны и эстетичны для глаз. Это можно заметить по спиралевидному расположению цветков и листьев.
Где в реальной жизни используется золотое сечение?
Существует множество применений золотого сечения в области искусства и архитектуры. Многие архитектурные чудеса были построены, чтобы отразить золотое сечение в своей структуре. Такие художники, как Лео да Винчи, Рафаэль, Сандро Боттичелли и Жорж Сера, использовали это как атрибут в своих работах. Его можно использовать для изучения структуры многих объектов в нашей повседневной жизни, которые напоминают определенный узор.
Кто открыл золотое сечение?
Древнегреческие математики первыми упомянули о золотом сечении в своих работах. Математики V века до нашей эры Гиппакус и Евклид внесли большой вклад в свои исследования по этому вопросу.
Что такое формула золотого сечения?
Формулу золотого сечения можно использовать для расчета значения золотого сечения. Формула для расчета золотого сечения дается как
1 + 1/ϕ = ϕ
, где ϕ обозначает золотое сечение.
Калькулятор золотого сечения – Академия старых мастеров
Урок рисования 4
« Назад к списку уроков рисования
Что такое золотое сечение
Золотое сечение (также известное как золотая середина, золотое сечение (лат. sectio aurea), крайнее и среднее отношение, медиальное сечение , божественная пропорция, божественное сечение (лат. sectio divina), золотая пропорция, золотой разрез и золотое число) — формула, управляющая искусством.
Это отношение может быть выражено следующим образом: Целое относится к большему в той же пропорции, в какой большее относится к меньшему .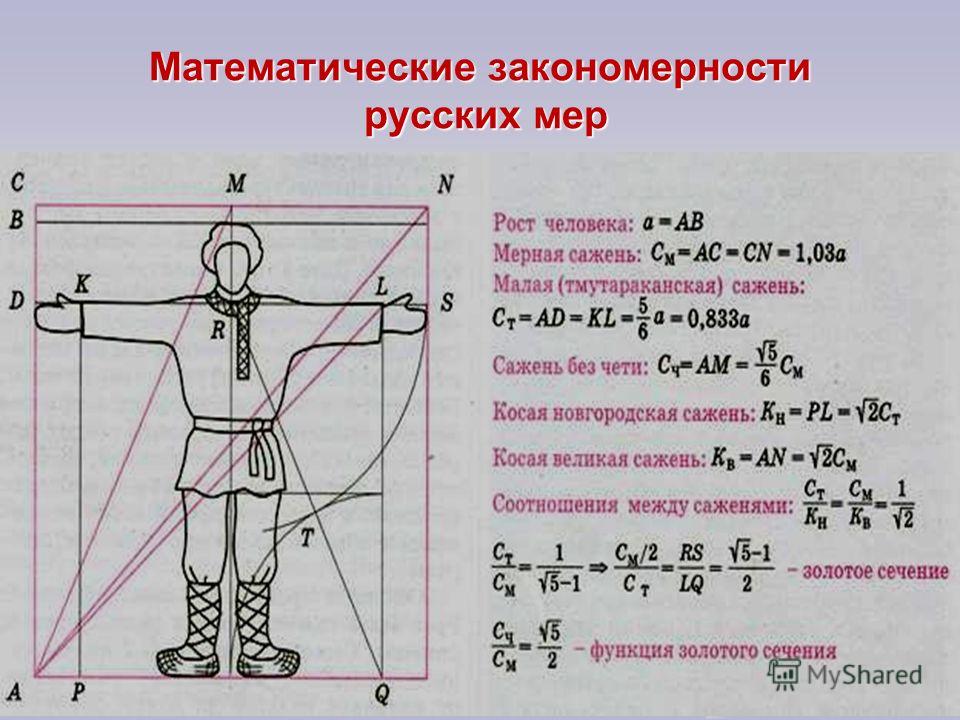
Она была математически описана Евклидом Александрийским (325–265 до н. э.), который разделил линию на ее «крайнее и среднее отношение»: к большим сегментам, так и больший к меньшему .
AB / AC = AC / CB = 1,61803
Значение золотого сечения, которое является пределом отношения последовательных чисел Фибоначчи, имеет значение приблизительно 1,61803.
Золотое сечение в искусстве
Искусство отражает природу и внутренний мир художника. То, что мы воспринимаем как прекрасное, пропорциональное и сбалансированное в природе, находит свое отражение в изобразительном искусстве, следуя тем же правилам божественных пропорций, что и вселенная. Отношения баланса, принципы гармонии и симметрии присутствуют в лучших произведениях изобразительного искусства. Итак, понимание и использование золотого сечения важно для любого художника.
Художник может использовать золотое сечение без ограничений. Божественная пропорция может быть реализована для разделения холста в соответствии с общим замыслом и содержанием, составления композиции всего произведения искусства или его частей, балансировки тональных значений или цветов.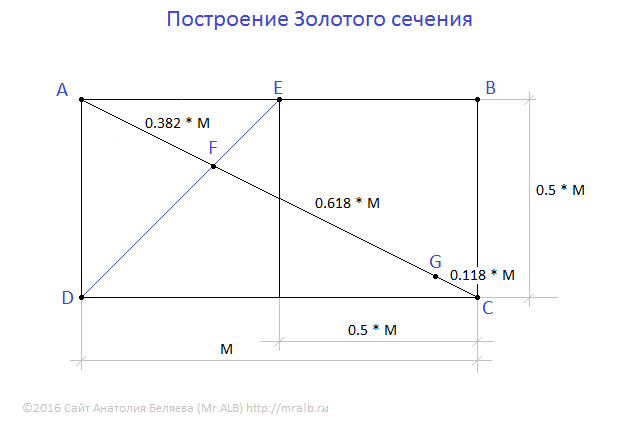
Чтобы сбалансировать элементы цвета, движения и содержания в форме холста, ключевые точки внимания или формы помещаются в определенные отношения с другими ключевыми точками. Делается ли это по какому-то внутреннему чувству гармонии или по расчету, знает только художник. Как наблюдатели, мы можем оценить окончательный результат, накладывая формы Божественной Пропорции, чтобы лучше осознавать общую динамику.
Калькулятор золотого сечения
Золотое сечение основано на соотношении, согласно которому целое можно сравнить с более длинной секцией точно так же, как более длинную секцию можно сравнить с 3 более короткой секция .
Калькулятор золотого прямоугольника
Золотой прямоугольник — это прямоугольник с размерами, соответствующими золотому сечению.